Statistiques et analyse de données

Antoine Géré

5 déc. 2025

Informations générales

Organisation


S2 S3 S4 S5
Cours magistraux 8 (12h) 8 (12h) 8 (12h) 8 (12h)
Travaux dirigés 8 (12h) 8 (12h) 8 (12h) 8 (12h)
tot. 16 (24h) 16 (24h) 16 (24h) 16 (24h)


  • Cours magistraux : pas besoin d’apporter son ordinateur
  • Travaux dirigés : venir avec son ordinateur


https://ant0in3g.github.io/sTa7.html \(\to\) check votre sticker !


Evaluations et projets de groupe



Evaluations

Pour chaque semestre :

  • Un examen de mi-semestre (1h30)
  • Un examen final (1h30)

Projets de groupe

Resources et dossier OneDrive

Resources

Dossier OneDrive partagé

Un dossier OneDrive a été partagé à chaque étudiant

To Do !

Synchronisez ce dossier sur votre ordinateur OU créez un raccourci sur votre propre OneDrive

Introduction aux statistiques avec R

coming !

Statistiques descriptives

coming !

Notions de probabilités

Combinatoire


Objectif de la combinatoire

Dénombrer des objets dans un ensemble fini.


Soit \(E_n\) un ensemble de \(n\) éléments.


Le nombre de manières de :


Ordonner (ou numéroter) les éléments de \(E_n\) est :

\[n!=1 \times 2 \cdots \times n \]


Choisir \(p\) éléments ordonnés dans \(E_n\) sans répétition , est :

\[ \begin{aligned} A_n^p & =n(n-1) \cdots(n-p+1) \\ & =\frac{n!}{(n-p)!} \end{aligned} \] (sans répétition : on ne peut reprendre un élément déjà choisi)


Choisir \(p\) éléments NON ordonnés dans \(E_n\) sans répétition est :

\[\binom{p}{n}=\frac{A_n^p}{p!}=\frac{n!}{p!(n-p)!} \] C’est aussi le nombre de parties à \(p\) éléments dans \(E_n\).


Choisir \(p\) éléments ordonnés dans \(E_n\) avec répétition est :

\[n^p \] (avec répétition : on est autorisé à reprendre un élément déjà choisi)


Choisir \(p\) éléments non ordonnés dans \(E_n\) avec répétition est :

\[\Gamma_n^p=\binom{p}{n+p-1}\] (avec répétition : on est autorisé à reprendre un élément déjà choisi)


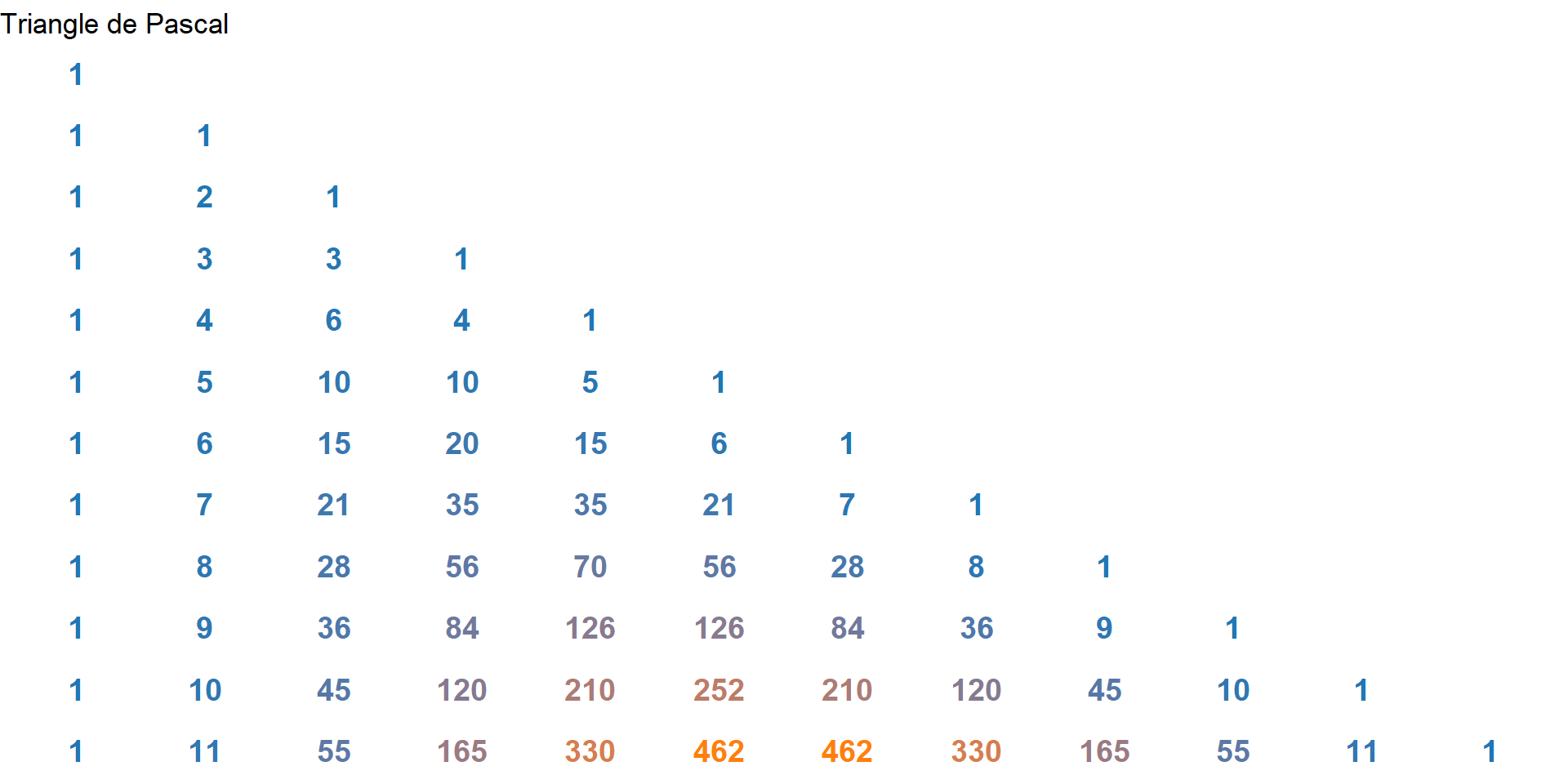
Le triangle de Pascal permet de calculer simplement le coefficient binomial \(\binom{n}{k}\). On choisit la ligne correspondant à \(n\) et la colonne correspondant à \(k\), et le nombre à leur intersection est le coefficient binomial.


Exemple :

\[\binom{7}{3} = 35\]

Expériences aléatoires, ensembles et evenements


Definition : Expérience aléatoire

Une expérience aléatoire est une expérience :

  • qui peut être répétée
  • qui a plusieurs résultats possibles
  • dont le résultat est imprévisible

Exemples :

  • lancé d’un dé à 6 faces
  • observation de l’état de germination d’une plante


Definition : Évènement élémentaire

Un évènement élémentaire est le résultat d’une expérience aléatoire

Exemples :

  • Obtenir 3 lors du lancé d’un dé à 6 faces
  • Être germée


Definition : Ensemble fondamental - Univers

  • Ensemble de tous les résultats possibles (évènements élémentaires) d’une expérience aléatoire.
  • On le note \(\Omega\)

Exemple : lancé d’un dé à 6 faces, \(\Omega=\{1,2,3,4,5,6\}\)


Propriété

  • \(\Omega\) peut être :

    • un ensemble fini

      Exemple : état de la germination, \(\Omega=\{\) germée, Non germée \(\}\)

    • un ensemble infini dénombrable

      Exemple : nombre de lancés avant d’obtenir face, \(\Omega=\{1,2, \ldots\}\)

    • un ensemble infini indénombrable

      Exemple : mesure du taux d’humidité dans un laboratoire

  • \(\Omega\) discret : \(\Omega\) fini ou infini dénombrable

  • \(\Omega\) continu : \(\Omega\) infini indénombrable


Definition : Évènement (non élémentaire)

Un événement (non élémentaire) est un sous-ensemble de \(\Omega\).

Exemple :

  • Un évènement A «Obtenir un résultat strictement supérieur à 4 lors du lancé d’un dé à 6 faces» \[A=\{5,6\}\]


Évènements particuliers :

  • L’évènement total \(\Omega\) est certain :

  • L’ensemble vide \(\varnothing\) est un évènement impossible


Opérations sur les évènements

Union

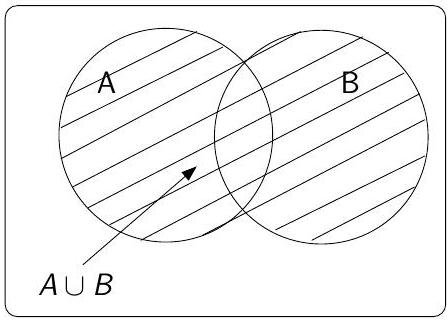
  • Notation : \(A \cup B\)

  • Définition : l’événement \(A \cup B\) est réalisé dès que \(A\) ou \(B\) est réalisé


Intersection

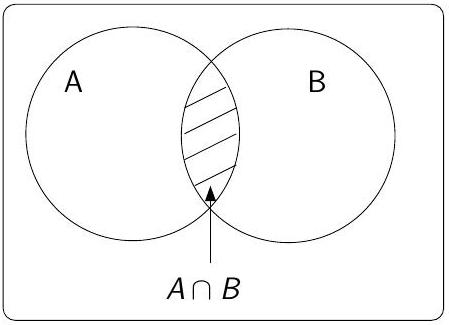
  • Notation : \(A \cap B\)
  • Définition : l’événement \(A \cap B\) est réalisé dès que \(A\) est \(B\) sont réalisés dans la même expérience


Complémentaire

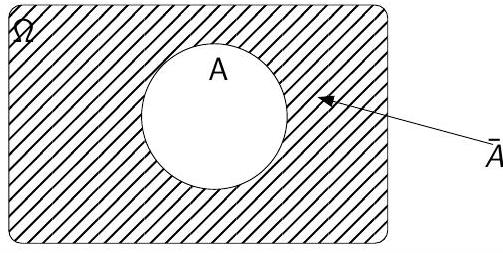
L’événement complémentaire de \(A\), noté \(\overline{A}\) contient tous les éléments de \(\Omega\) qui ne sont pas dans \(A\).

En particulier

  • \(\overline{A \cap B}=\overline{A} \cup \overline{B}\)
  • \(\overline{A \cup B}=\overline{A} \cap \overline{B}\)


Évènements incompatibles

A et B sont dits incompatibles si \(A \cap B=\varnothing\)


Système complet d’évènements

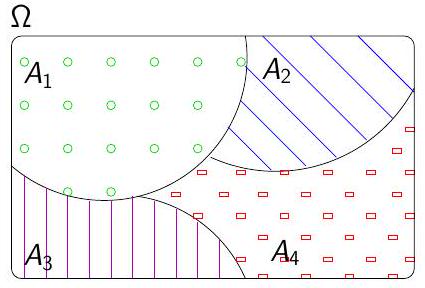
On appelle système complet d’évènements toute partition de \(\Omega\), c’est à dire tout ensemble d’évènement ( \(A_{i}\) ) tel que :

  • Pour tout \(i\), on a \(A_{i} \neq \varnothing\)
  • Pour tout \(i, j\), on a \(A_{i} \cap A_{j}=\varnothing\) (évènements 2 à 2 incompatibles)
  • \(\bigcup_{i} A_{i}= A_1 \cup A_2 \cup \dots = \Omega\)

Introduction aux probabilités

Definition

On appelle probabilité sur \(\Omega\), une application \(P\) qui à tout évènement \(A\) de \(\Omega\), associe un réel \(\mathrm{P}(A)\) positif ou nul tel que :

  • \(\mathrm{P}(\Omega)=1\)
  • Si A et B sont incompatibles alors \(\mathrm{P}(A \cup B)=\mathrm{P}(A)+\mathrm{P}(B)\)


Propriétés :

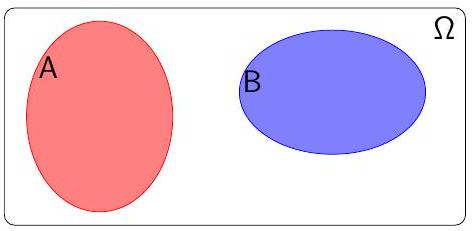
\[ \begin{gathered} \mathrm{P}(A)=\frac{\text { Surface de } \mathrm{A}}{\text { Surface de } \Omega} \\ \mathrm{P}(\Omega)=1(\text { définition }) \quad \mathrm{P}(\varnothing)=0 \end{gathered} \]

  • \(\mathrm{P}(A) \leq 1\)

  • Si \(A_{1}, A_{2}, \ldots A_{n}\) sont \(n\) évènements incompatibles 2 à 2 alors \[\mathrm{P}\left(A_{1} \cup A_{2} \cup \ldots \cup A_{n}\right)=\sum_{i=1}^{n} \mathrm{P}\left(A_{i}\right)\]

  • \(\mathrm{P}(\overline{A})=1-\mathrm{P}(A)\)

  • Pour 2 évènements \(A\) et \(B\), \[\mathrm{P}(A \cup B)=\mathrm{P}(A)+\mathrm{P}(B)-\mathrm{P}(A \cap B)\]

Probabilité conditionnelle

Soit \(B\) un évènement de probabilité non nulle


Probabilité conditionnelle

Pour tout évènement \(A\), on appelle probabilité conditionnelle de \(A\) sachant que \(B\) est réalisé, le réel \(\mathrm{P}(A \mid B)\) défini par : \[\mathrm{P}(A \mid B)=\frac{\mathrm{P}(A \cap B)}{\mathrm{P}(B)}\]

Exemples :

  • Probabilité, pour un vache (B), d’avoir un veau male (A)

  • Probabilité d’avoir un fort rendement (A) sachant que le taux de précipitation est faible


Propriétés :

Une probabilité conditionnelle vérifie toutes les propriétés des probabilités, en particulier

  • \(\mathrm{P}(\Omega \mid B)=1\)
  • \(\mathrm{P}(\varnothing \mid B)=0\)
  • \(\mathrm{P}(\overline{A} \mid B)=1-\mathrm{P}(A \mid B)\)
  • \(\mathrm{P}\left(A_{1} \cup A_{2} \mid B\right)=\mathrm{P}\left(A_{1} \mid B\right)+\mathrm{P}\left(A_{2} \mid B\right)-\mathrm{P}\left(A_{1} \cap A_{2} \mid B\right)\)


De la définition des probabilités conditionnelles, on déduit :

\[ \mathrm{P}(A \cap B)=\mathrm{P}(B) \times \mathrm{P}(A \mid B) \]


Partition de \(\Omega\) en 2

\(A\) et \(\overline{A}\) forment un système complet d’évènements.

Pour tout évènement \(B\) on peut écrire \[\mathrm{P}(B)=\mathrm{P}(B \mid A) \times \mathrm{P}(A)+\mathrm{P}(B \mid \overline{A}) \times \mathrm{P}(\overline{A})\]

Démonstration :

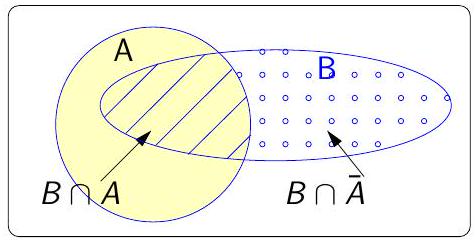
\[ \begin{aligned} & B=B \cap \Omega=B \cap(A \cup \overline{A}) \\ & B=(B \cap A) \cup(B \cap \overline{A}) \end{aligned} \]

\(B \cap A\) et \(B \cap \overline{A}\) sont incompatibles donc \[\mathrm{P}(B)=\mathrm{P}(B \cap A)+\mathrm{P}(B \cap \overline{A})\]

On applique la formule des probabilités composées et on obtient

\[ \mathrm{P}(B)=\mathrm{P}(B \mid A) \times \mathrm{P}(A)+\mathrm{P}(B \mid \overline{A}) \times \mathrm{P}(\overline{A}) \]


Le théorème de Bayes

Astuce

  • Soient \(\left\{A_{1} ; A_{2} ; \ldots ; A_{n}\right\}\) un système complet d’évènements et \(B\) un évènement de probabilité non nulle.

  • Pour tout \(j \in\{1 ; 2 ; \ldots ; n\}\), on a :

\[ \mathrm{P}\left(A_{j} \mid B\right)=\frac{\mathrm{P}\left(A_{j}\right) \times \mathrm{P}\left(B \mid A_{j}\right)}{\mathrm{P}(B)}=\frac{\mathrm{P}\left(A_{j}\right) \times \mathrm{P}\left(B \mid A_{j}\right)}{\sum_{i=1}^{n} \mathrm{P}\left(A_{i}\right) \times \mathrm{P}\left(B \mid A_{i}\right)} \]


Exemple d’application

  • Etude du comportement des vaches en stabulation

  • \(C\) : La variable indicatrice de l’évènement La vache est en colère

  • \(M\) : La variable indicatrice de l’évènement La vache meugle

On a :

  • la probabilité que la vache meugle sachant qu’elle est en colère est de \(90 \%\)

  • la probabilité que la vache meugle sachant qu’elle n’est pas en colère est de \(25 \%\)

On veu

\[\begin{align*} P(C\mid M) &= \frac{P(M\mid C) \ P(C)}{P(M\mid C) P(C) + P(M \mid C) P(C)} \\[4pt] &= \frac{0.9 \times 0.33}{0.9 \times 0.33+0.25 \times 0.67} \\[5pt] P(C\mid M) &= 0.64 \end{align*}\]

donc la vache ayant meuglé, on estime la probabilité qu’lle ait été en colère à \(64 \%\)

Indépendance

Définition 1

Deux évènements \(A\) et \(B\) de probabilité non nulle sont indépendants (relativement à la probabilité \(P\)) si et seulement si

\[ \mathrm{P}(A \mid B)=\mathrm{P}(A) \]

La réalisation d’un des évènements n’a pas d’influence sur la probabilité de réalisation de l’autre évènement

Définition 2

Deux évènements \(A\) et \(B\) de probabilité non nulle sont indépendants (relativement à la probabilité \(P\)) si et seulement si

\[ \mathrm{P}(A \cap B)=\mathrm{P}(A) \times \mathrm{P}(B) \]

Théorème

\(A\) et \(B\) indépendants \(\Leftrightarrow A\) et \(\overline{B}\) indépendants \(\Leftrightarrow \overline{A}\) et \(B\) indépendants \(\Leftrightarrow \overline{A}\) et \(\overline{B}\) indépendants

Épreuves indépendantes

  • On parlera d’épreuves indépendantes lorsque le résultat d’une des épreuves n’a aucune influence sur les résultats des autres épreuves

  • Utile pour la constitution de n -échantillons

Variables aléatoires définitions


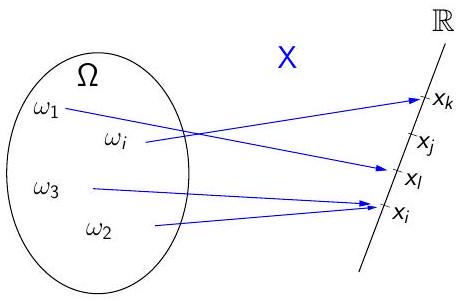
  • À chaque événement élémentaire \(\omega\) correspond un nombre réel \(x\).

  • \(x\) est la réalisation de la variable \(X\) pour l’événement \(\omega\)

  • Il n’y a pas obligatoirement autant de valeurs possibles \(x\) que d’événements élémentaires !


Notations :

  • Les variables aléatoires sont notées avec des lettres majuscules : \(X, Y, Z, \ldots\)

  • Les valeurs possibles ou réalisations d’une variable aléatoire sont notées avec des lettres minuscules : \(x_i, a, z, \ldots\)


Propriétés :

Si \(X\) et \(Y\) sont des variables aléatoires définies sur \(\Omega\) alors :

  • \(X+Y\) est une variable aléatoire

  • \(X \times Y\) est une variable aléatoire

  • \(\forall \lambda \in \mathbb{R}, \lambda X\) est une variables aléatoires


Deux types de variables aléatoires

Variable aléatoire discrète

Elle prend un nombre fini ou infini dénombrable de valeurs possibles

Exemples :

  • Résultat d’un lancé de dé

  • Nombre d’arosage fait sur une culture


Variable aléatoire continue

Elle prend un nombre infini indénombrable de valeurs possibles

Exemples :

  • Taux d’humidité

  • Poids des pommes récoltées

Variables aléatoires discrètes

  • Une variable aléatoire est dite discrète si elle ne peut prendre ses valeurs que dans un ensemble discret, une suite de valeurs isolées \[\left\{x_1, x_2, \ldots x_i, \ldots\right\}\]


Loi de Bernouilli

  • Utiliser dès qu’une situation est analogue au modèle suivant :

    • On considère une urne avec des boules blanches en proportion \(p\) et noires en proportion \(q=1-p\).

    • On tire une boule.

    • On pose : \(X=1\) si la boule est blanche, et \(X=0\) sinon.

    • La loi de probabilité de cette variable aléatoire est: \[p(X=1)=p, \qquad p(X=0)=q=1-p\]

# Paramètre de la loi Bernoulli
p <- 0.3

# Valeurs possibles
x <- c(0, 1)

# Probabilités
proba <- c(1 - p, p)

# Tracé
barplot(proba, 
        names.arg = x, 
        col = "skyblue", 
        main = "un exemple de loi de Bernoulli sur R", 
        xlab = "x", 
        ylab = "P(X=x)")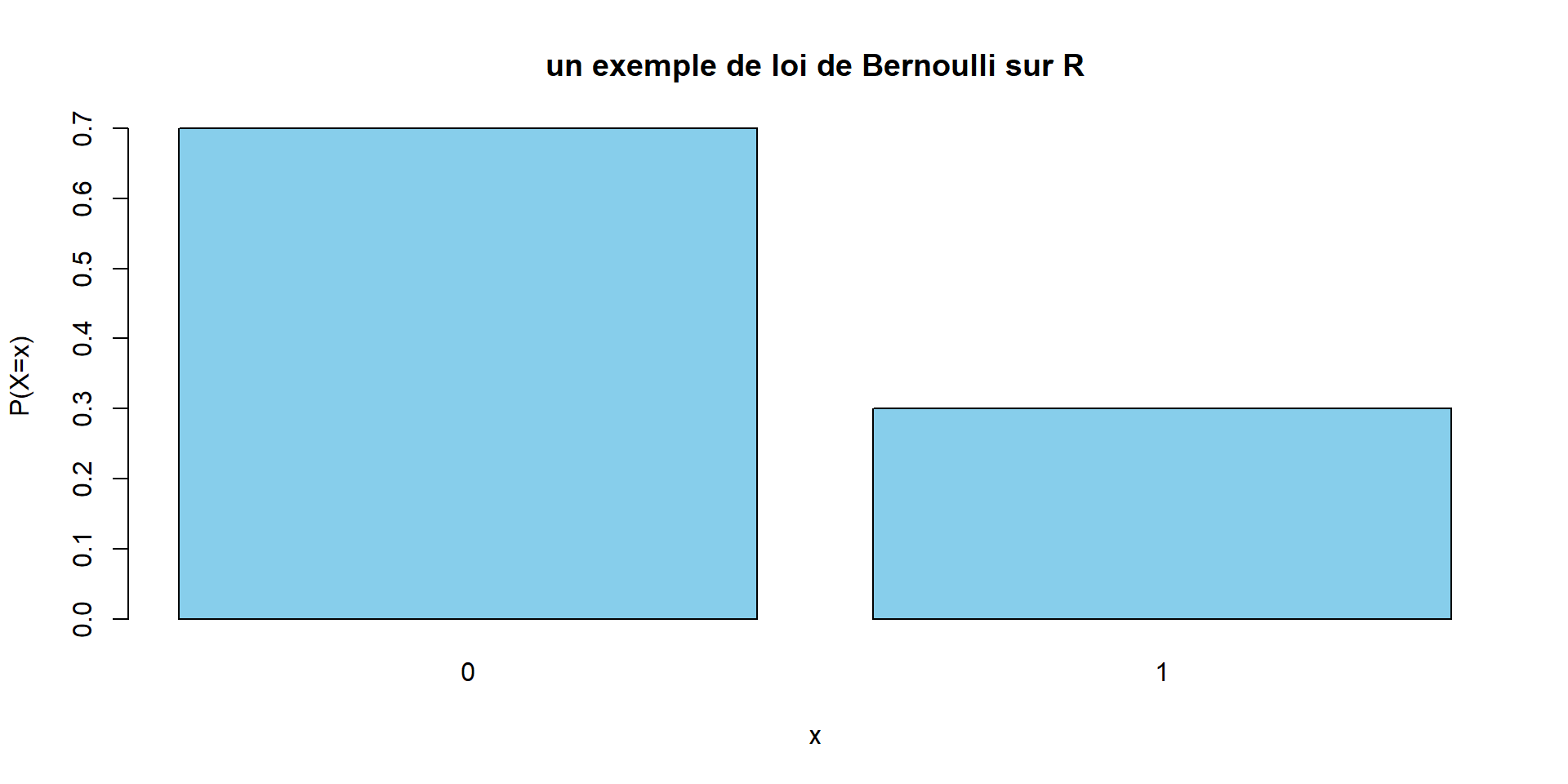


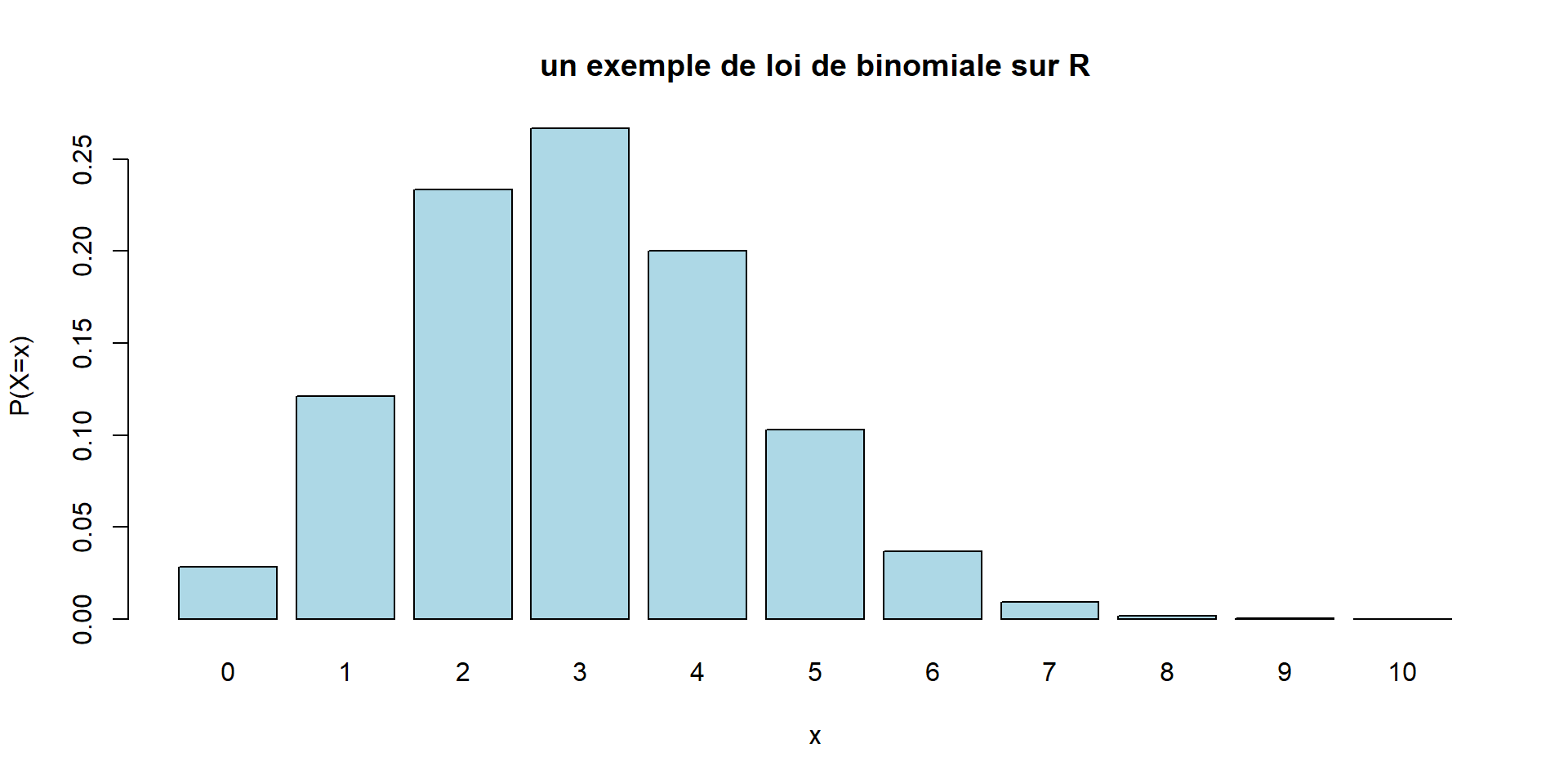
Loi binomiale

  • Le modèle correspondant est le suivant :
    • dans la même urne, on tire \(n\) boules avec remise.
    • \(X\) est le nombre de boules blanches obtenues.
    • On a alors \[P(X=k) = \binom{k}{n} \ p^k q^{n-k}\]

Remarque : Si le nombre de boules dans l’urne est très grand et le nombre de tirages petit, on peut considérer que le fait de remettre ou non les boules change peu le résultat. On pourra alors utiliser la loi binomiale même s’il n’y a pas remise.


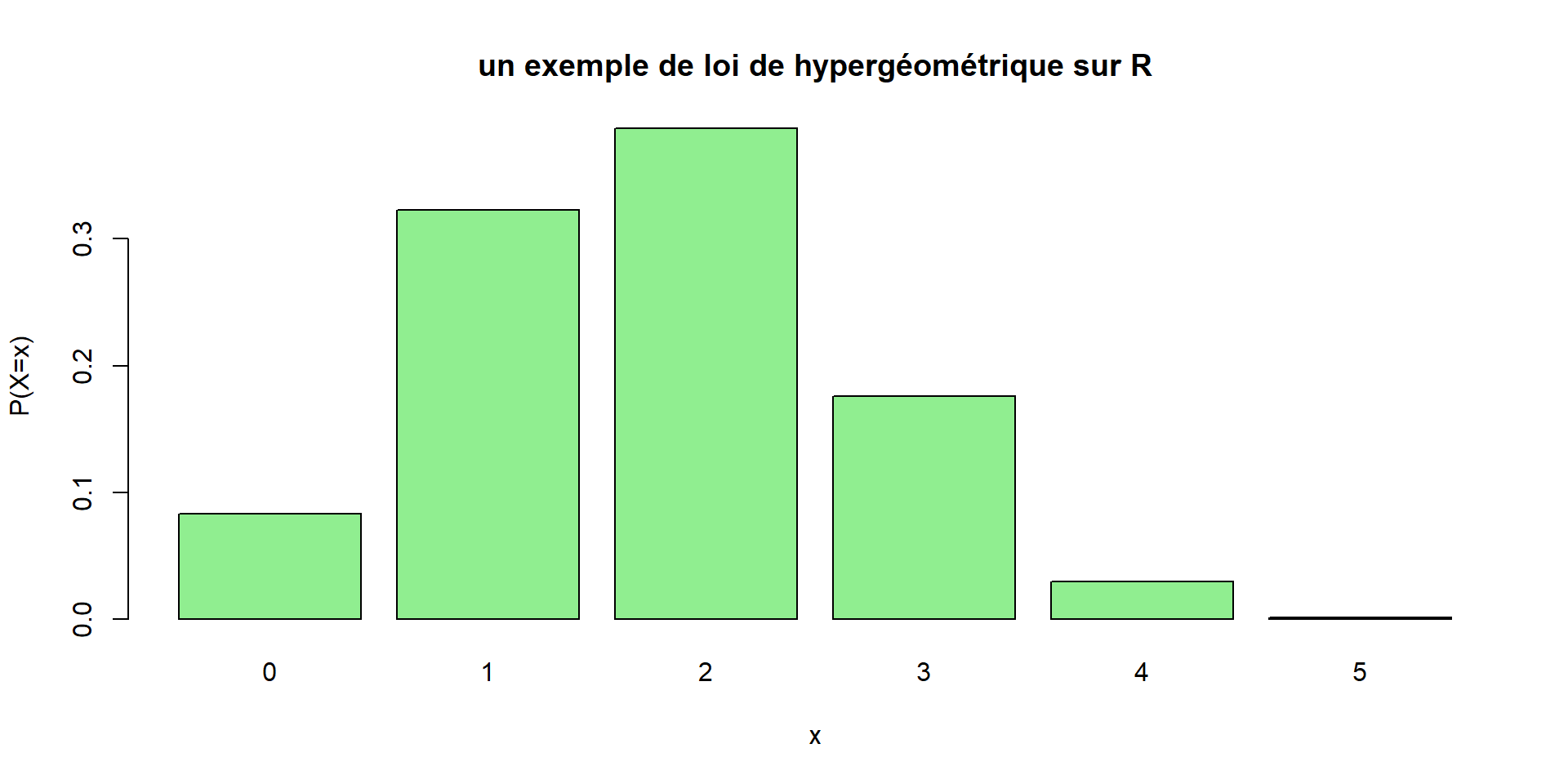
Loi hypergéométrique

Pas exigible.


  • Le même modèle est le même que pour la loi binomiale, mais on fait les \(n\) tirages sans remise.

  • \(X\) est encore le nombre de boules blanches obtenues.

  • Soit \(a\) le nombre de boules blanches dans l’urne, \(b\) le nombre de boules noires, et \(a+b\) le nombre total.

  • On a (en raisonnant sur le nombre de cas favorables) : \[P(X=k)=\frac{\binom{k}{a} \binom{n-k}{b}}{\binom{n}{a+b}}\]

Remarque : Contrairement à la loi binomiale, l’utilisation de cette loi nécessite la connaissance du nombre total \(a+b\) d’éléments dans l’urne.


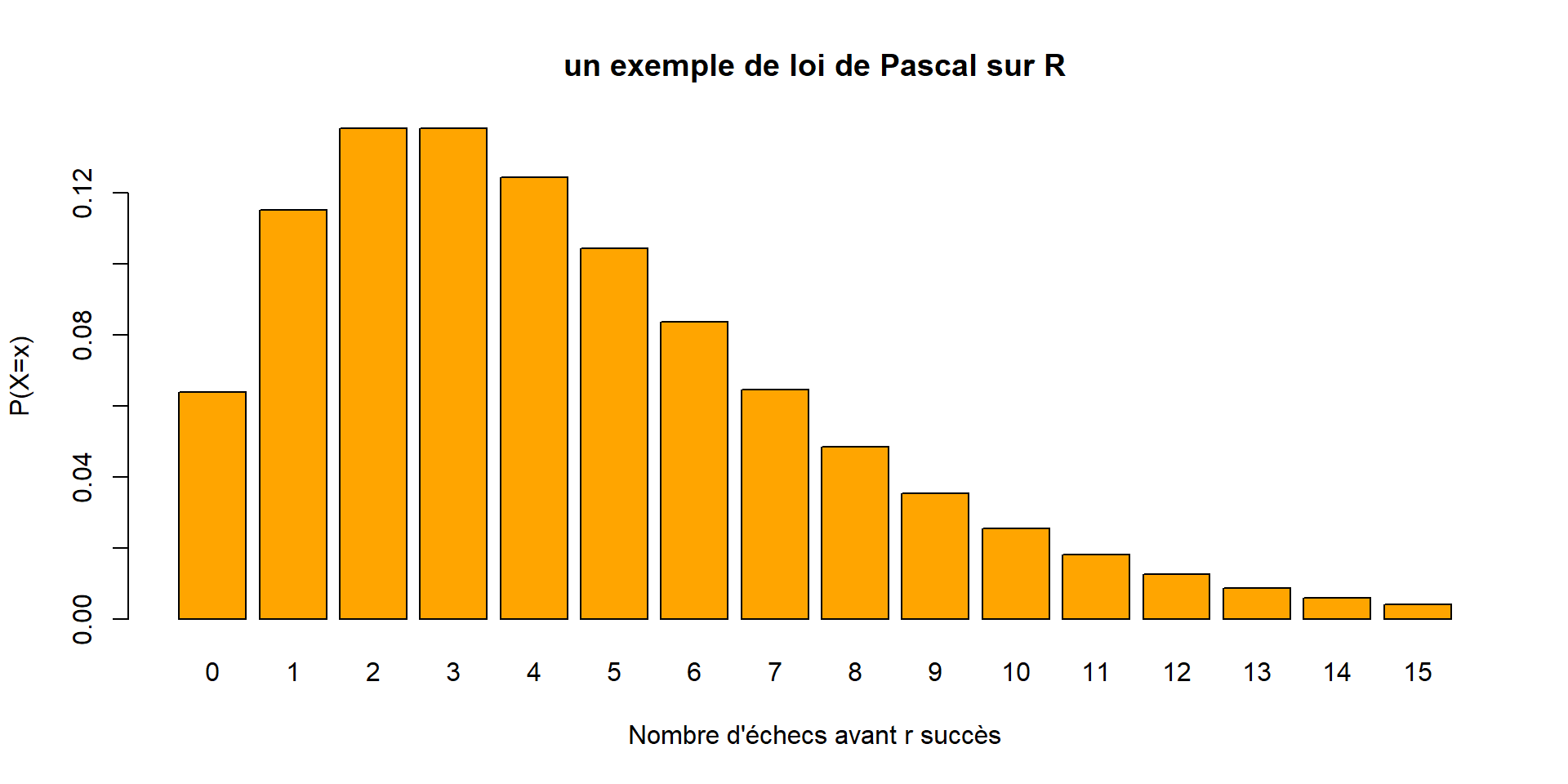
Loi de Pascal

Pas exigible.


  • Dans la même urne, on tire maintenant des boules avec remise jusqu’à obtenir \(r\) boules blanches (\(r\) fixé).

  • \(X\) est le nombre de tirages nécessaires pour obtenir \(r\) boules blanches.

  • On a, pour tout \(k \geq r\) : \[P(X=k)=\binom{r-1}{k-1} p^r q^{k-r}\]


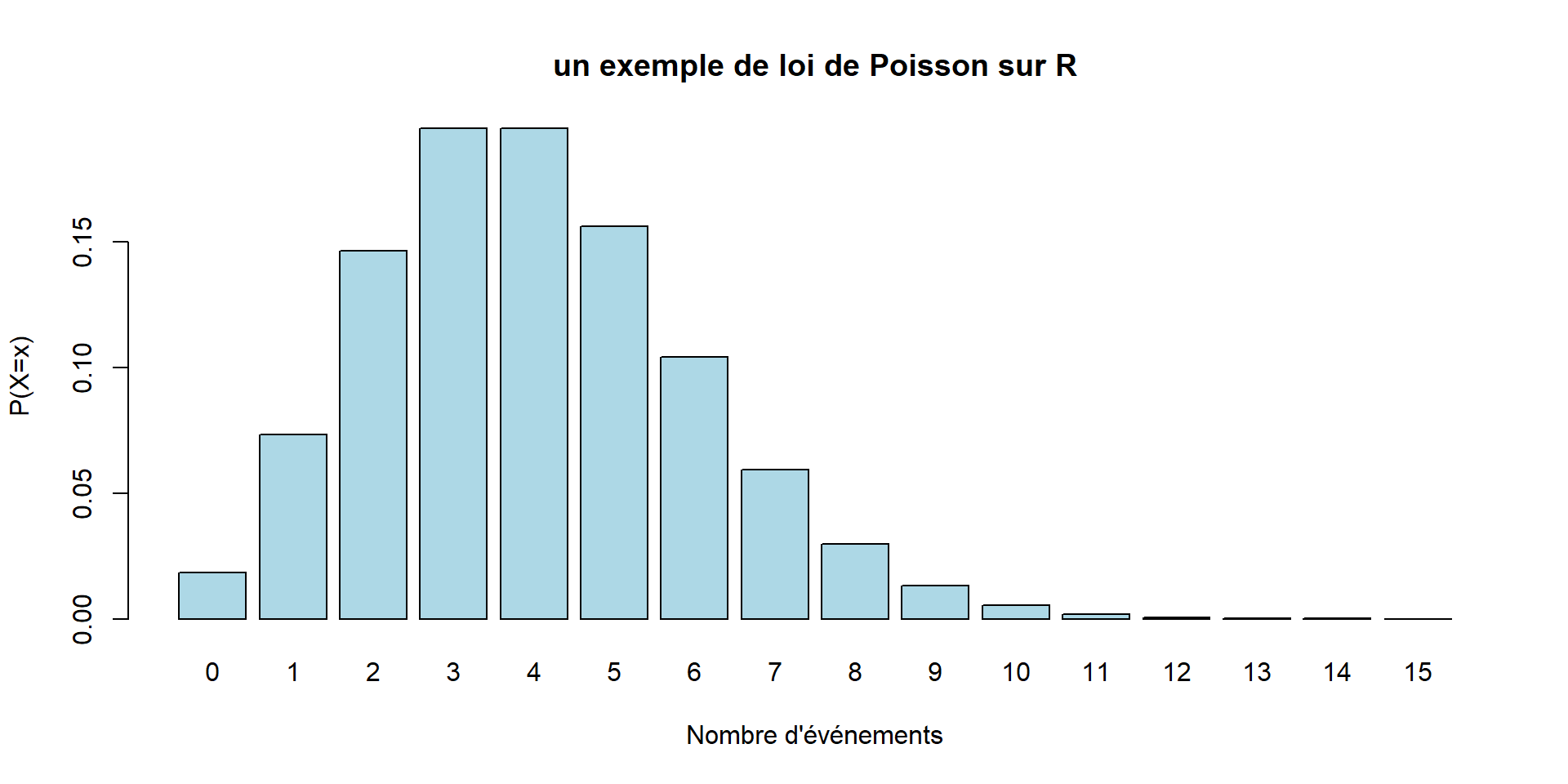
Loi de Poisson

Pas exigible.


  • Utiliser dans une situation consistant à compter le nombre d’évènements pendant une durée donnée.

  • La variable \(X\) est le nombre d’évènements apparus pendant cette durée.

  • On a pour tout \(k \geq 0\) : \[p(X=k)=e^{-\lambda} \frac{\lambda^k}{k!}\]

où \(\lambda\) est un paramètre positif fixé.


Paramètres d’une variable aléatoire discrète


Espérance Variance
Loi de Bernouilli \(\displaystyle p\) \(\displaystyle p q\)
Loi binomiale \(\displaystyle n p\) \(\displaystyle n p q\)
Loi hypergéométrique \(\displaystyle n p\) \(\displaystyle n p q \ \frac{a+b-n}{a+b-1}\)
Loi de Pascal \(\displaystyle \frac{r}{p}\) \(\displaystyle \frac{q}{p^2}\)
Loi de Poisson \(\displaystyle \lambda\) \(\displaystyle \lambda\)


Ce tableau n’est pas connaitre !

Variables aléatoires continues


  • Une variable aléatoire est dite continue lorsqu’elle peut prendre ses valeurs dans tout un intervalle de \(\mathbb{R}\).

  • On se limite à l’étude de la loi normale.


La loi normale \(\mathcal{N}\left(\mu,\sigma\right)\)

Si \(X\) suit une loi normale, on lui associe une courbe :

\[y = \frac{1}{\sigma \sqrt{2 \pi}} \ \exp \left(-\frac{(x-\mu)^2}{2 \sigma^2}\right)\]

cette relation n’est pas à retenir !

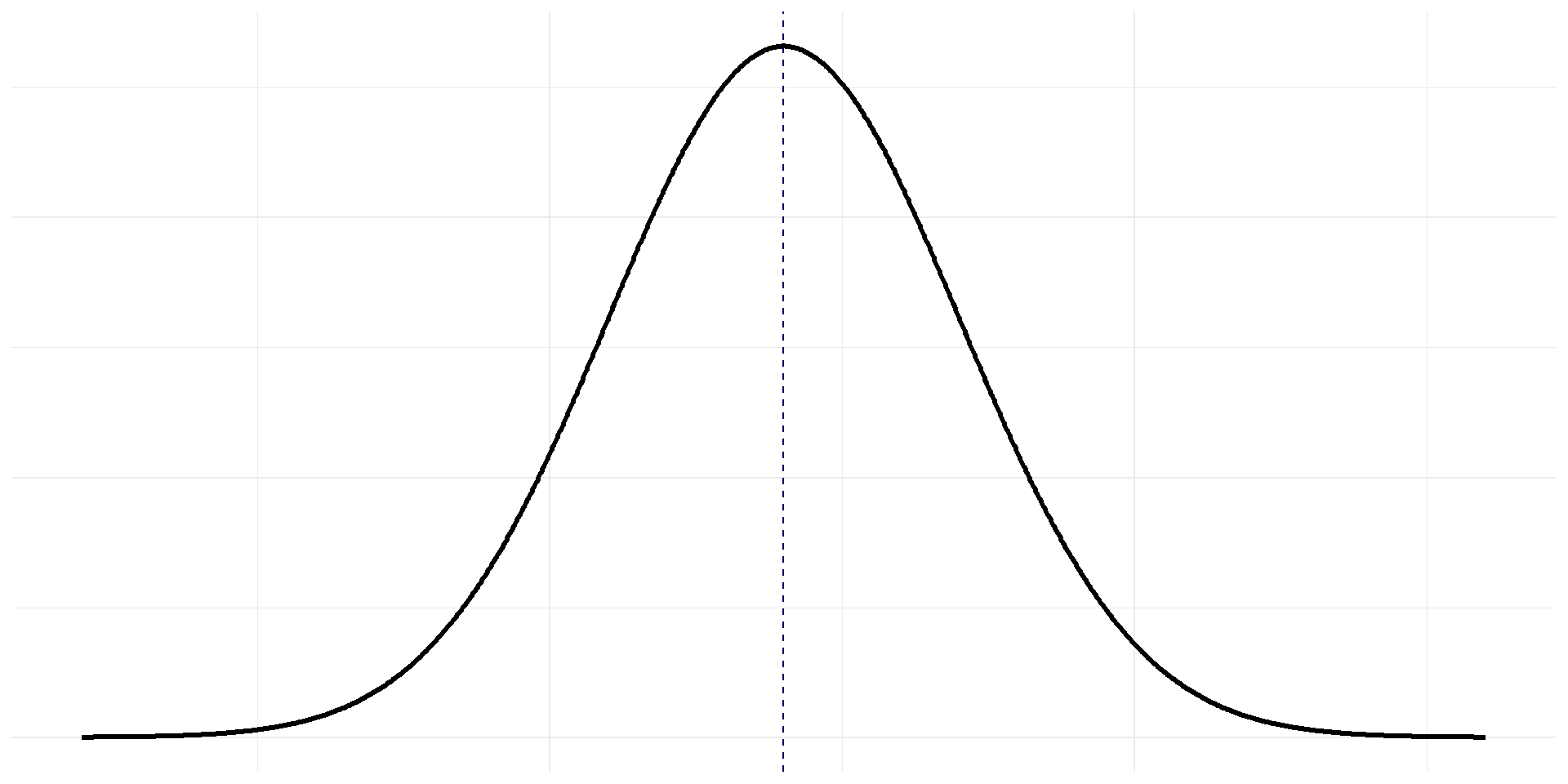
  • cette courbe est symétrique par rapport à l’axe \(x= \mu\)

  • à retenir : courbe en “forme de cloche”

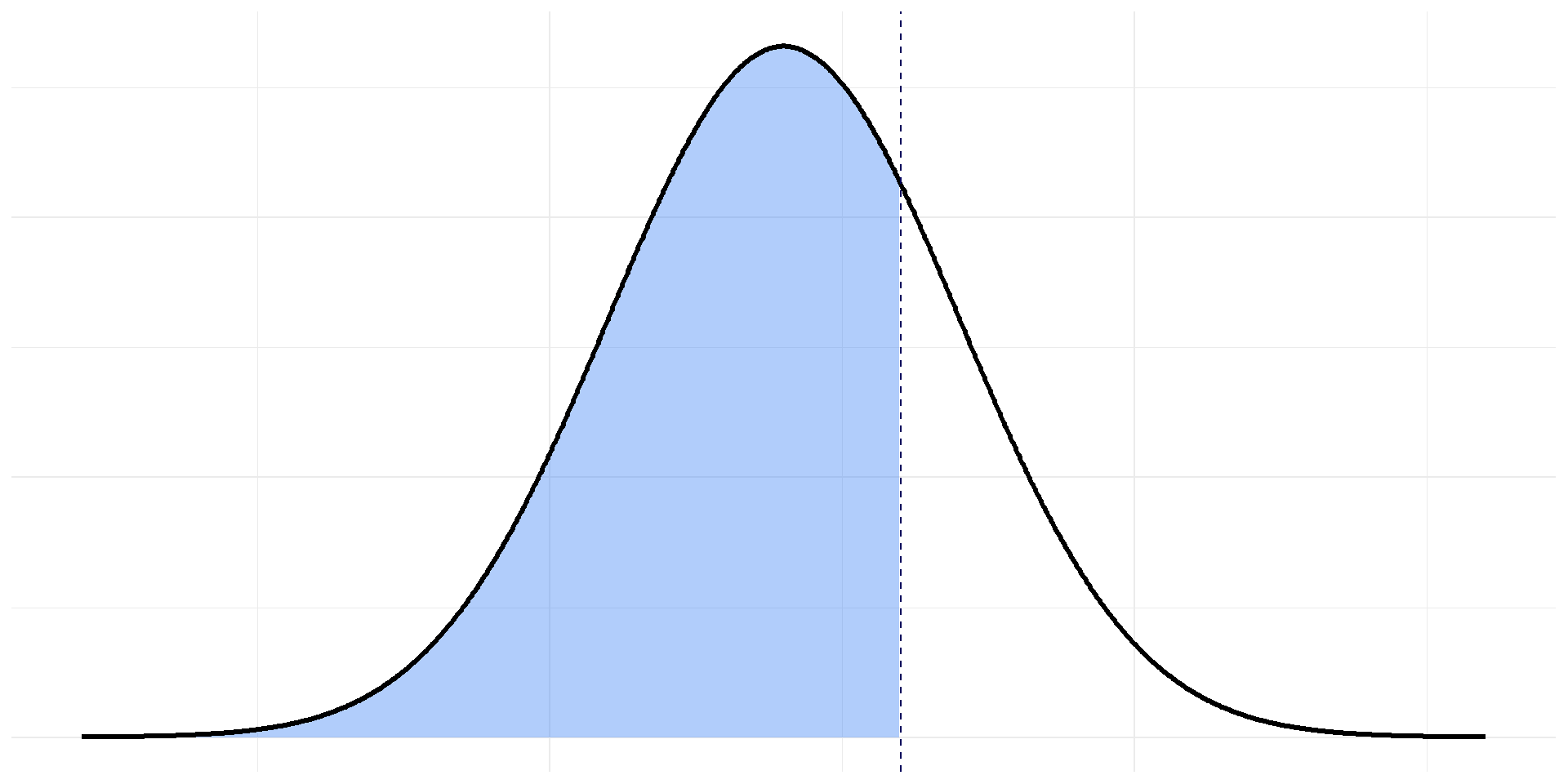
  • l’axe en pointillé est \(x=a\)

  • l’aire bleutée représente : \(\displaystyle P(X\leq a)\)


Important

  • Pour chaque \(\mu\), \(\sigma\), il existe une loi normale de moyenne \(\mu\) et d’écart-type \(\sigma\).

  • On la note \(\mathcal{N}(\mu, \sigma)\)

  • Cas particulier : \(\mu=0\) et \(\sigma=1\) désignera la loi normale centrée réduite : \(\mathcal{N}(0,1)\).

  • L’aire sous la courbe de \(-\infty\) à \(+\infty\) est égale à 1 ! \[P\left(-\infty \leq X \leq +\infty\right)=1\]


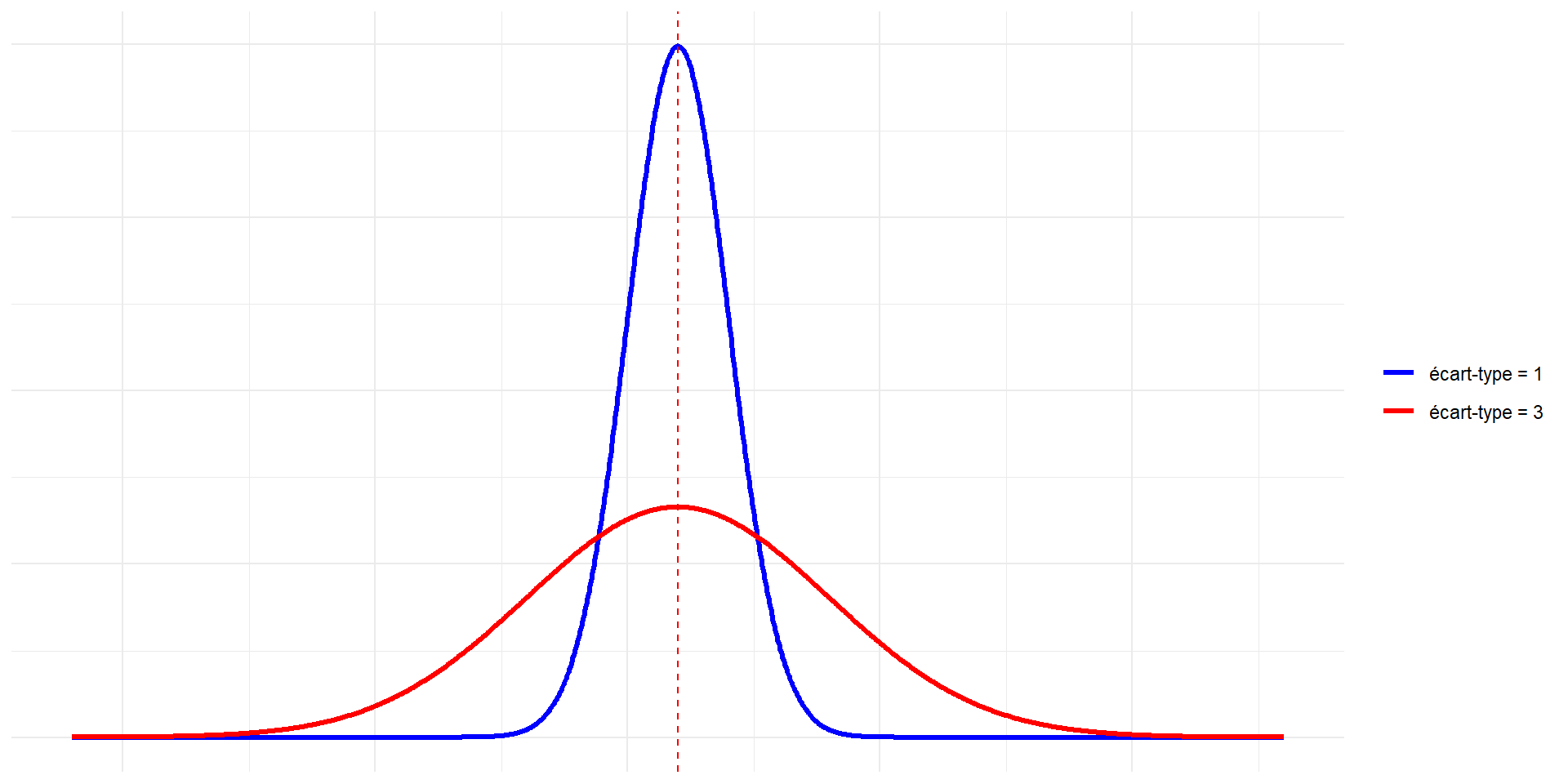
Propriétés de la loi normale

Exemple de lois normales avec des moyennes différentes et le même écart-type

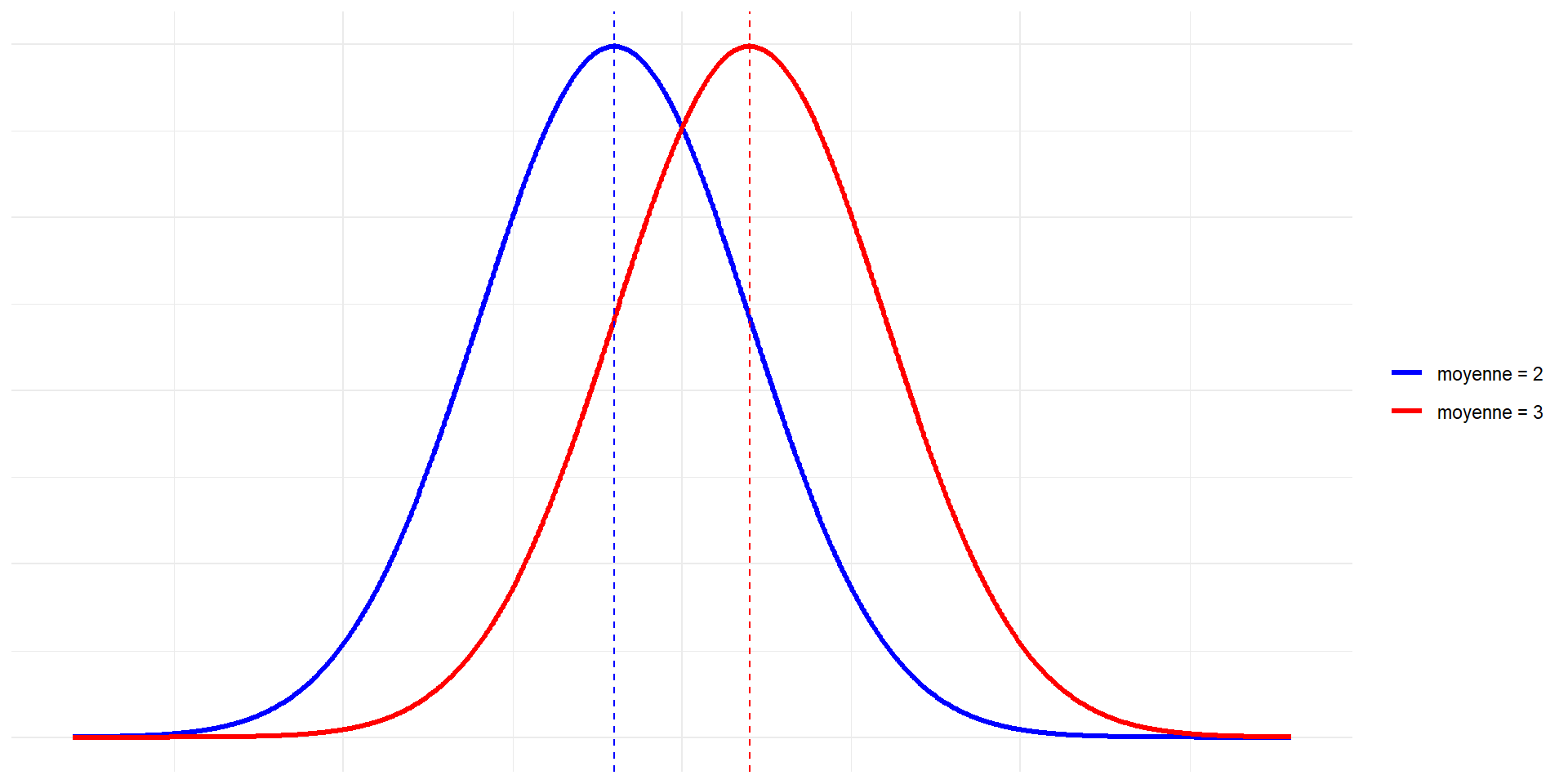
Exemple de lois normales avec même moyenne et des écart-types différents


Calculs pratiques pour la loi normale centrée réduite

\(X\) suit une loi normale centée réduite \(\mathcal{N}(0,1)\)


  • On va utiliser la table de la loi normale.

  • Sur la table de la loi normale on lit (\(a>0\)):

\[P(X \leq a) = \Pi(a)\]

Exemple 1 : \(P(X \leq a)\)

  • On suppose qu’une certaine variable \(X\) suit la loi normale centée réduite \(\mathcal{N}(0,1)\).

  • Pour quelle proportion d’individus est-ce que \(X \leq 1,56\) ?

  • On cherche \(\displaystyle P(X \leq 1,56) = \Pi(1,56)\).

  • On cherche \(1,56\) dans la table

  • On peut alors lire \(\Pi(1,56) = 0,9406\)

  • Pour \(94,06 \%\) des individus, la variable \(X\) est inférieure à \(1,56\).


Exemple 2 : \(P(X \geq a)\)

  • On suppose qu’une certaine variable \(X\) suit la loi normale centée réduite \(\mathcal{N}(0,1)\).

  • Pour quelle proportion d’individus est-ce que \(X \geq 1,49\) ?

  • On cherche \(\displaystyle P(X \geq 1,49)\).

  • On écrit d’abord \[P(X \geq 1,49)=1-P(X \leq 1,49)=1-\Pi(1,49)\]

  • On cherche \(1,49\) dans la table

  • On peut alors lire \(\Pi(1,49) = 0,9319\)

  • Donc \(P(X \geq 1,49) = 1 - 0.9319 = 0,0681\)

  • Pour \(6,81 \%\) des individus, la variable \(X\) est supérieure à \(1,49\).


Exemple 3 : \(P(X \leq -a)\)

  • On suppose qu’une certaine variable \(X\) suit la loi normale centée réduite \(\mathcal{N}(0,1)\).

  • Pour quelle proportion d’individus est-ce que \(X \leq -1,1\) ?

  • On cherche \(\displaystyle P(X \leq-1,1)\)

  • On remarque (par symétrie) que \[P(X \leq -1,1) = P(X \geq 1,1) = 1 - P(X \leq 1,1)\]

  • On cherche \(1,49\) dans la table

  • On peut alors lire \(\Pi(1,1) = 0,8643\)

  • Donc \(P(X \leq -1,1) = 1 - 0.8643 = 0,1357\)

  • Pour \(13,57 \%\) des individus, la variable \(X\) est inférieure à \(-1,1\).


Exemple 4 : \(P(X \geq -a)\)

  • On suppose qu’une certaine variable \(X\) suit la loi normale centée réduite \(\mathcal{N}(0,1)\).

  • Pour quelle proportion d’individus est-ce que \(X \geq -0,76\) ?

  • On cherche \(\displaystyle P(X \geq -0.76)\)

  • On remarque (par symétrie) que \[P(X \geq -0,76) = P(X \leq 0,76)\]

  • On cherche \(0,76\) dans la table

  • On peut alors lire \(\Pi(0,76) = 0,7764\)

  • Donc \(P(X \geq -0,76) = 0,7764\)

  • Pour \(77,64 \%\) des individus, la variable \(X\) est supérieure à \(-0,76\).


Exemple 6 : Lecture inversée de la table

  • On suppose qu’une certaine variable \(X\) suit la loi normale centée réduite \(\mathcal{N}(0 ; 1)\).

  • On souhaite déterminer \(t\)t tel que \(\displaystyle P( X \leq t) = 0,9664\).

  • On cherche dans la table la probabilité \(0,9664\)

  • En lisant les coefficients sur la ligne et la colonne de \(0,9664\), on détermine \(t\)

  • On trouve \(t=1,83\)

  • Donc \(P(X \leq 1,83)=0,9664\).


Calculs pratiques pour une loi normale quelconque

  • \(X\) suit une loi normale quelconque \(\mathcal{N}(\mu,\sigma)\)

  • Pour les calculs avec \(\mathcal{N}(\mu, \sigma)\), on se ramène à la loi \(\mathcal{N}(0,1)\)

Centrer et réduire une loi normale

Si
\[X \sim \mathcal{N}(\mu, \sigma)\] alors \[\frac{X-\mu}{\sigma} \sim \mathcal{N}(0,1)\]

On dit que l’on centre et réduit \(X\).

\[ \]


Exemple 5 :

  • On suppose qu’une certaine variable \(X\) suit la loi normale \(\mathcal{N}(11 ; 2)\).

  • Pour quelle proportion d’individus est-ce que \(X \leq 14\) ?

  • On cherche \(P(X \leq 14)\).

  • On centre et on réduit \(X\) : \[Z= \frac{X-11}{2} \sim \mathcal{N}(0,1)\]

  • On a alors \[P(X \leq 14) = P\left(\frac{X-11}{2} \leq \frac{14-11}{2}\right) = P(Z \leq 1,5)\]

  • On cherche \(1,5\) dans la table.

  • On peut alors lire \(\Pi(1,5) = 0,9332\)

  • Donc \(P(Z \leq 1,5) = 0,9332\)

  • Donc \(P(X \leq 14) = 0,9332\)

  • Pour \(93,32 \%\) des individus, la variable \(X\) est supérieure à \(14\).


Autres lois continues

Pas exigible.


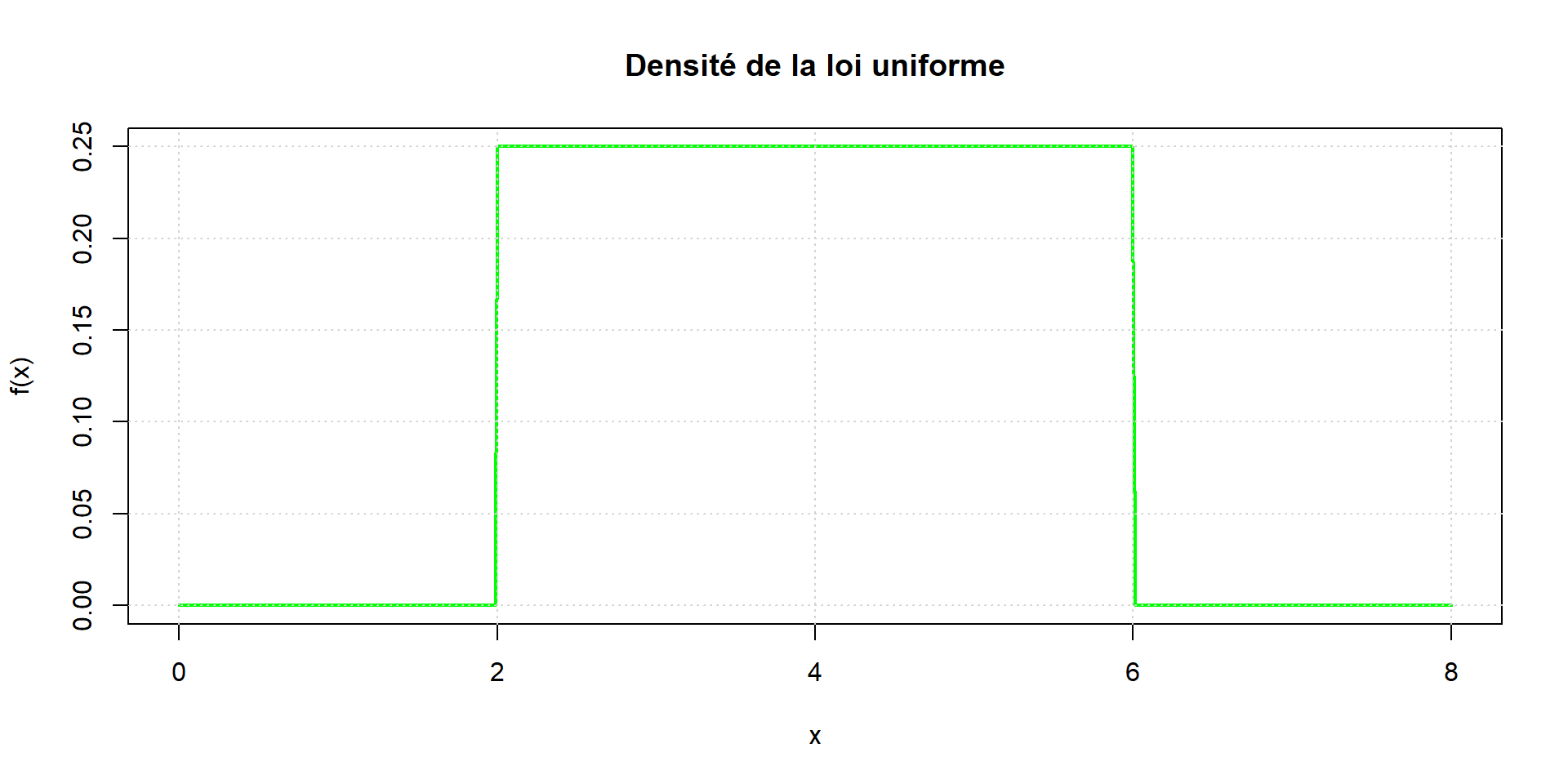
Loi uniforme

  • La probabilité que la valeur de \(X\) tombe dans un intervalle de longueur fixée reste la même quelque soit cet intervalle inclus dans \([a, b]\).

  • On doit alors avoir \(f(x)\) constante, donc \[f(x)-\frac{1}{b-a}\] sur \([a, b]\), et \(f(x)=0\) en dehors, afin d’obtenir une aire totale de \(1\)

  • On a \(E(X) = \dfrac{a+b}{2}\) et \(\sigma(X) = \sqrt{\dfrac{(b-a)^2}{12}}\)


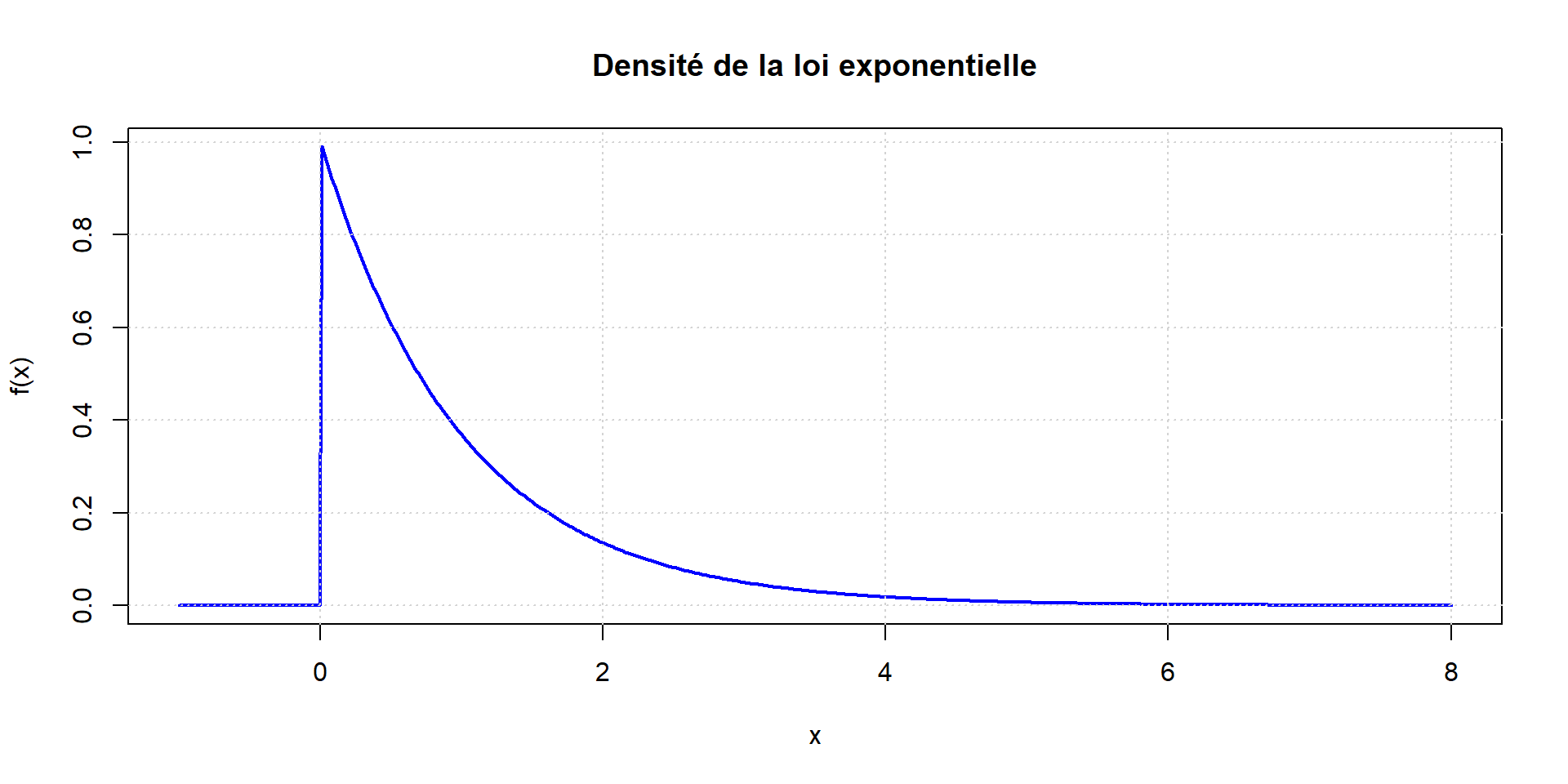
Loi exponentielle

  • Souvent utilisée pour des questions de fiabilité

  • Elle est définie pour \(x \geq 0\) par \[f(x)=\frac{1}{a} e^{-x / a}\] et \(f(x)=0\) pour \(x<0\)

  • On a \(E(X) = a\) et \(\sigma(X) = a\)

Echantillonnage et estimation

Notions sur l’échantillonnage

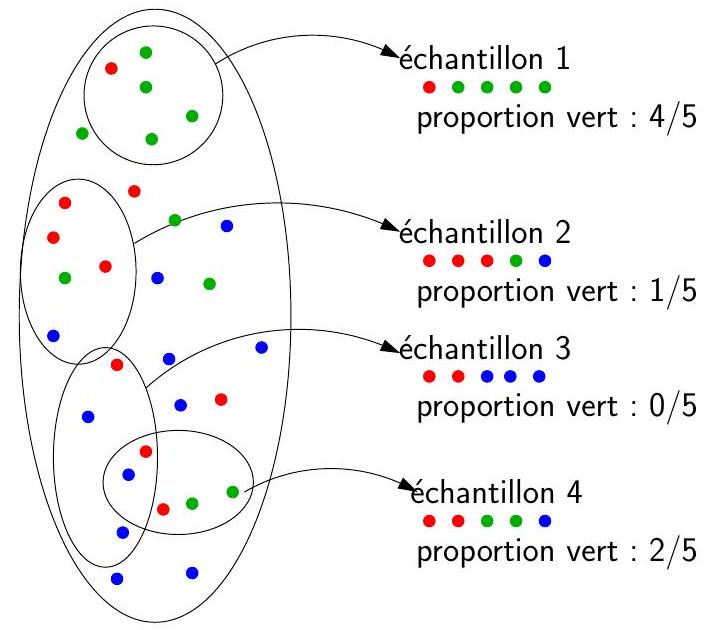
Population \(\to\) proportion vert : 10/30


  • Le choix d’une taille de l’échantillon n’est pas simple

  • Plus il y a d’individus, plus le degré de précision de l’enquête sera fort

  • Les contraintes pratiques nous obligent à limiter le nombre d’individus

  • 2 types de méthodes d’échantillonnage :

    • échantillonnage probabiliste
    • échantillonnage NON probabiliste

  • Objectif : le plus représentatif possible !

Les méthodes d’échantillonnage probabilistes


Exemple utilisé pour illustrer ces méthodes :

  • Il y a environ 3 millions étudiants en France.

  • On souhaite savoir si les étudiants sont satifaits ou non de leur formation.

  • Ne pouvant pas accéder à tous les étudiants, on décide de former un échantillon de 100 000 étudiants (taille arbitraire) le plus représentatif possible.


Échantillonnage aléatoire simple

  • Tous les individus ont une chance égale d’être sélectionné.

  • Constitution de l’échantillon :

    • échantillonnage aléatoire simple “sans remise” : cas le plus courrant

    \(\to\) quand on sélectionne uniquement des individus différents

    • échantillonnage aléatoire simple “avec remise” : si l’on n’a pas accès à beaucoup d’individus

    \(\to\) quand un ou plusieurs individus peuvent être sélectionnés plusieurs fois


Exemple :

Avec un échantillonnage aléatoire simple avec remise, on sélectionne les 100 000 étudiants au hasard parmi les 3 millions.



Échantillonnage systématique

  • Constitution de l’échantillon :
    • on numérote tous les individus de la population (dans l’ordre que l’on veut)
    • on tire un individu au hasard parmi les premiers numéros, disons le \(i\)-ème
    • on se fixe un écart de \(m\) individus
    • on compléte l’échantillon en prenant les individus correspondants aux numéros :
      • \(i+m\)
      • \(i+2 m\)
      • \(i+3 m\)
      • et ainsi de suite


Exemple :

  • On numérote tous les étudiants

  • On choisit, par exemple, le troisième de la liste

  • On se fixe un écart de 200

  • On complète l’échantillon les étudiants numérotés

    • 203
    • 403
    • 603
    • et ainsi de suite jusqu’au 100 000-ème étudiant



Échantillonnage aléatoire avec probabilité inégale

L’échantillonnage aléatoire avec probabilités inégales part du principe que certains individus ont plus ou moins de chances d’être sélectionnés


Exemple :

  • On peut, par exemple, pondérer la probabilité de sélectionner un étudiant en fonction de la taille de son université

  • On peut alors accorder plus d’importance aux étudiants des petites universités pour augmenter leurs chances de figurer dans l’échantillon



Échantillonnage stratifié

  • Une strate est un groupe homogène d’individus dans une population

  • Si la population peut se diviser en plusieurs strates pertinentes dans le contexte, alors il est judicieux de les prendre en compte pour constituer un échantillon le plus représentatif possible.

  • L’échantillonnage stratifié consiste à faire :

    • un échantillonnage aléatoire simple (sans remise) dans chaque strate,
    • et de combiner tous les échantillons obtenus pour constituer l’échantillon final


Exemple :

  • On peut différencier les étudiants de Licence ou en Master

  • Avec un échantillonnage aléatoire simple sans remise, on peut constituer :

    • un échantillon dans la strate des étudiants en Licence, disons de taille 70 000

    • et un autre dans la strate des étudiants en Master, disons 30 000

  • L’échantillon final est constitué de ces deux échantillons.



Échantillonnage par grappes

  • Si la population se divise en plusieurs groupes d’individus, l’échantillonnage en grappes consiste à :
    • choisir au hasard plusieurs de ces groupes
    • une fois un groupe sélectionné, on considère tous ses individus
    • l’échantillon est donc l’ensemble des individus des groupes sélectionnés
  • Préférable de choisir un grand nombre de petits groupes, plutôt qu’un petit nombre de gros groupes


Exemple :

  • On sélectionne au hasard quelques universités

  • On considère tous les étudiants de celles-ci

  • Le nombre d’universités sélectionnées est de telle sorte à ce que la taille de l’échantillon ne soit pas trop éloignée de 100 000



Échantillonnage à deux degrés

  • L’échantillonnage à deux degrés est une version “améliorée” de l’échantillonnage en grappes

  • Constitution de l’échantillon :

    • on choisit au hasard des groupes
    • dans chacun des groupes choisis, on sélectionne des individus avec une méthode probabiliste

  • Avantages :

    • Plus souple sur le nombre de groupes à choisir
    • On peut aller à plus de deux degrés en continuant le processus de sélection des individus.


Exemple :

  • On sélectionne au hasard quelques universités

  • On effectue un échantillonnage aléatoire simple des étudiants dans chacune de ces universités.

  • L’échantillon final se compose de tous les individus finalement sélectionnés.

  • On s’arrange pour que la taille de l’échantillon ne soit pas trop éloigné de 100 000



Échantillonnage à deux phases

  • L’échantillonnage à deux phases permet :
    • de révéler des strates inconnues au premier abord,
    • de les utiliser pour obtenir un échantillon représentatif.
  • Constitution de l’échantillon :
    • on choisit au hasard des individus (comme avec un échantillonnage aléatoire simple)
    • on pose une (ou plusieurs) question discriminante à ces individus
    • on sélectionne les individus en fonction de leurs réponses (on choisit uniquement les individus qui ont formulé une certaine réponse, ou on crée des strates dans l’échantillon déjà formé, et on poursuit avec un sondage stratifié ou autre, etc.).


Exemple :

  • Avec un échantillonnage aléatoire simple, on forme

    • un premier échantillon d’étudiants,

    • puis on leur pose une unique question : “Avez-vous été assidus pendant les cours?”

    • On ne conserve que les étudiants qui ont répondu “oui”

    • On peut alors concentrer l’enquête de satisfaction de la formation que sur eux

Les méthodes d’échantillonnage NON probabilistes


Exemple utilisé pour illustrer ces méthodes :

  • Il y a environ 3 millions étudiants en France.

  • On souhaite savoir si les étudiants sont satifaits ou non de leur formation.

  • Ne pouvant pas accéder à tous les étudiants, on décide de former un échantillon de 100 000 étudiants (taille arbitraire) le plus représentatif possible.


Échantillonnage de commodité ou à l’aveuglette

L’échantillonnage de commodité ou à l’aveuglette consiste à sélectionner les individus dont on a immédiatement accès, sans discrimination particulière.


Exemple :

  • On va dans les universités les plus proche

  • On demande aux étudiants que l’on croise s’ils sont contents ou non de leur formation.

  • On constitu ainsi un échantillon de taille 100 000 sans trop de problème



Échantillonnage volontaire

  • L’échantillonnage volontaire considère les individus qui sont volontaires pour participer à l’enquête

  • Les individus se sélectionnent eux-mêmes.

  • Il peut y avoir une récompense en jeu.


Exemple :

  • Un café est offert aux 100 000 premiers étudiants de France qui répondront à la question :

“Êtes-vous contents de votre formation ?”



Échantillonnage au jugé

  • L’échantillonnage au jugé consiste à sélectionner uniquement les individus qui semblent être dans le cœur de cible de l’enquête.

  • Il repose sur des critères subjectifs et des idées préconçues.


Exemple :

  • On va dans les universités les plus proche

  • On demande aux étudiants que l’on croise et qui paraissent sérieux s’ils sont contents ou non de leur formation.

\(\to\) très subjectif !

  • On constitue ainsi un échantillon de taille 100 000 sans trop de problème

\(\to\) pas représentatif de l’ensemble des étudiants de France



Échantillonnage par quotas

  • L’échantillonnage par quotas repose sur un résultat statistique déjà connu sur la répartition de la population

    OU sur un quota d’individus que l’on impose

  • Partant d’une taille d’échantillon choisie, l’idée est de former un échantillon d’individus dont l’appartenance aux groupes respecte ces pourcentages

  • Il n’y a pas de règle sur la méthode pour choisir les individus, du moment que les quotas sont respectés


Exemple :

  • On sait qu’il y a :

    • \(~ 70 \%\) étudiants en Licence
    • et \(~ 30 \%\) d’étudiants en Master

  • On se fixe une taille d’échantillon de 100 000

  • On sélectionne :

    • \(100 000 \times 0.7 = 70 000\) étudiants en Licence
    • et \(100 000 \times 0.3 = 30 000\) étudiants en Master
    • La sélection de ces étudiants peut se faire comme on veut



Échantillonnage boule de neige ou de réseaux

  • Lorsque l’on s’intéresse à une population très spécifique, on peut utiliser l’échantillonnage boule de neige

  • Cela consiste à interroger des individus par la méthode au jugé, puis d’interroger leur connaissances (amis, collègues, etc.)

Echantillonnage en pratique

On s’interesse ici uniquement à l’échantillonage aléatoire simple.

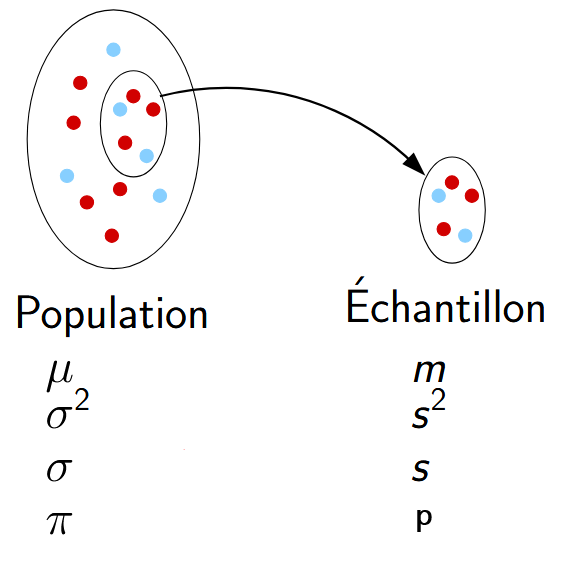
  • Echantilon de taille \(n\)

  • Paramètres dans la population : Connues

  • Paramètres dans l’échantillon : Inconnues

  • Objectif : estimer les paramètres dans l’échantillon

    • pour les moyennes : \(\quad\mathcal{N}\left(m,\dfrac{\sigma}{\sqrt{n}}\right)\) \[m = \mu \quad \mbox{ et } \quad s_m = \dfrac{\sigma}{\sqrt{n}}\]
    • pour les proportions : \(\quad\mathcal{N}\left(p,\sqrt{\dfrac{p(1-p)}{n}}\right)\) \[p = \pi \quad \mbox{ et } \quad s_p = \sqrt{\dfrac{p(1-p)}{n}}\]


Exemple 1 :

Selon une étude menée depuis quatre ans, la moyenne des istomien-nes à leur mémoire de fin d’étude s’élève à 13, avec un écart type de 3. On choisit d’une manière aléatoire un échantillon de 20 étudiants.

Question

Calculer la probabilité que cet échantillon ait une moyenne \(>11\).


Solution

cf. correction manuscrite


Exemple 2 :

Selon les archives de l’ISTOM, le \(\%\) des filles primées lors de la remise des diplômes s’élève à \(60 \%\). On choisit d’une manière aléatoire un échantillon de 30 étudiants primés.

Question

Calculer la probabilité que cet échantillon soit composé de moins de \(55 \%\) de filles.


Solution

cf. correction manuscrite

Estimateurs et estimations

Estimateur et estimations ponctuelles

  • \(\theta\) désigne le paramètre à estimer
  • \(\theta: \mu, \sigma, \pi\), médiane, …
  • Soit \(T\) un estimateur de \(\theta\)

Estimateur

Un estimateur de \(\theta\), noté \(T\), est une variable aléatoire exprimée en fonction des variables aléatoires d’échantillon \(X_{i}\). On a donc : \[T=f\left(X_{1} ; X_{2} ; \ldots ; X_{n}\right)\]

Exemple : cas de \(M\), l’estimateur de \(\mu\)

\[ M=\frac{X_{1}+X_{2}+\ldots+X_{n}}{n} \]

Estimation

Une estimation de \(\theta\) est un nombre calculé en fonction des valeurs \(x_{i}\) observées dans l’echantillon. On a donc \[t=f\left(x_{1} ; x_{2} ; \ldots ; x_{n}\right)\]

Exemple : cas de l’estimation de \(\mu\)

\[ m=\frac{x_{1}+x_{2}+\ldots+x_{n}}{n} \]


Notations :

paramètre théorique estimateur estimation
\(\mu\) \(M\) \(m\)
\(\sigma^{2}\) \(S^{2}\) \(s^{2}\)
\(\sigma\) \(S\) \(s\)
\(\pi\) \(P\) \(p\)


Qualité d’un estimateur

Biais d’un estimateur

Le biais d’un estimateur \(T\) de \(\theta\) est défini par \[b(T) = E(T) - \theta\]

Variance d’un estimateur

Plus la variance d’un estimateur \(T\), notée \(\operatorname{var}(T)\), est faible, plus les estimations sont peu dispersées !


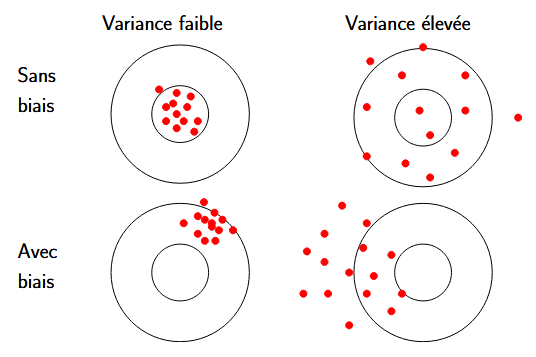
Erreur quadratique moyenne

  • L’erreur quadratique moyenne d’un estimateur \(T\) de \(\theta\) est défini par \[EQM(T) = \operatorname{var}(T) + b(T)^2\]

  • Un bon estimateur a une erreur quadratique moyenne la plus faible possible, idéalement \[E Q M \xrightarrow[n \rightarrow+\infty]{ } 0\]


Estimateur de l’espérance \(\mu\)

Moyenne d’échantillon ou moyenne empirique

\(M\) : moyenne d’échantillon ou moyenne empirique (parfois notée \(\overline{X}\) )

\[M=\frac{X_{1}+X_{2}+\ldots+X_{n}}{n}\]

Expression de \(\mu_{M}\)

On sait que

\[ \mathrm{E}(a X+b Y)=a \times \mathrm{E}(X)+b \times \mathrm{E}(Y) \]

On peut donc écrire

\[ \begin{gathered} \mathrm{E}(M)=\mathrm{E}\left(\frac{X_{1}+X_{2}+\ldots+X_{n}}{n}\right) \\ \mathrm{E}(M)=\frac{1}{n} \times \mathrm{E}\left(X_{1}+X_{2}+\ldots+X_{n}\right) \\ \mathrm{E}(M)=\frac{1}{n}\left(\mathrm{E}\left(X_{1}\right)+\mathrm{E}\left(X_{2}\right)+\ldots+\mathrm{E}\left(X_{n}\right)\right) \\ \mathrm{E}(M)=\frac{1}{n} \times n \mu \\ \mathrm{E}(M)=\mu \end{gathered} \]

Expression de \(\sigma_{M}\)

On sait que si \(X\) et \(Y\) sont 2 variables aléatoires indépendantes : \[ \operatorname{var}(a X+b Y)=a^{2} \times \operatorname{var}(X)+b^{2} \times \operatorname{var}(Y) \]

donc

\[ \begin{gathered} \operatorname{var}(M)=\operatorname{var}\left(\frac{X_{1}+X_{2}+\ldots+X_{n}}{n}\right) \\ \operatorname{var}(M)=\frac{1}{n^{2}} \times \operatorname{var}\left(X_{1}+X_{2}+\ldots+X_{n}\right) \end{gathered} \] de plus comme les variables sont indépendantes on a \[ \begin{gathered} \operatorname{var}(M)=\frac{1}{n^{2}} \times\left(\operatorname{var}\left(X_{1}\right)+\operatorname{var}\left(X_{2}\right)+\cdots+\operatorname{var}\left(X_{n}\right)\right) \\ \operatorname{var}(M)=\frac{1}{n^{2}} \times n \sigma^{2} \\ \operatorname{var}(M)=\frac{\sigma^{2}}{n} \end{gathered} \]

Qualité de l’estimateur \(M\)

On a donc

\[ \mathrm{E}(M)=\mu \quad \text { et } \quad \operatorname{var}(M)=\frac{\sigma^{2}}{n} \quad \text { et } \quad \sigma_{M}=\frac{\sigma}{\sqrt{n}} \]

On a \[EQM(M) = \operatorname{var}(M) + b(M)^2 = \frac{\sigma^{2}}{n}+0 = \frac{\sigma^{2}}{n}\] donc

\[\lim _{n \rightarrow+\infty} EQM(M) =0\]

Important

\(M\) est donc un bon estimateur de l’espérance


Estimateur d’une proportion

  • Soit \(X\) une variable aléatoire modélisant le statut de germination d’une graine

  • Soit \(S_{n}\) une variable aléatoire modélisant le nombre de graines germées parmi un ensemble de \(n\) graines. \[S_n=\sum_{i=1}^{n} X_{i}\]

  • \(P\) est une variable aléatoire modélisant la proportion de graines germées \[P=\frac{S_{n}}{n}=\frac{\sum_{i=1}^{n} X_{i}}{n}\]

On admet que \(P\) suit approximativement une loi normale.

\[ \begin{gathered} \mathrm{E}(P)=\mathrm{E}\left(\frac{S_{n}}{n}\right)=\frac{1}{n} \times \mathrm{E}\left(S_{n}\right)=\frac{1}{n} \times n \pi=\pi \\ \operatorname{var}(P)=\operatorname{var}\left(\frac{S_{n}}{n}\right)=\frac{1}{n^{2}} \times \operatorname{var}\left(S_{n}\right)=\frac{1}{n^{2}} \times n \pi(1-\pi)=\frac{\pi \times(1-\pi)}{n} \end{gathered} \]

Qualité de l’estimateur \(P\)

On a

\[ \mathrm{E}(P)=\pi \quad \text { et } \quad \operatorname{var}(P)=\frac{\pi \times(1-\pi)}{n} \]

d’où

\[\begin{gathered} EQM(P) = \operatorname{var}(F) + b(F)^2 \\ EQM(P) = \operatorname{var}(F) + \mathrm{E}(\mathrm{F})-\pi \\ EQM(P) = \frac{\pi \times(1-\pi)}{n} + \pi - \pi \\ EQM(P) = \frac{\pi \times(1-\pi)}{n} \end{gathered}\]

On a donc

\[\lim _{n \rightarrow+\infty} EQM(P) =0\]

Important

\(F\) est donc un bon estimateur d’une proportion

Estimations en pratique

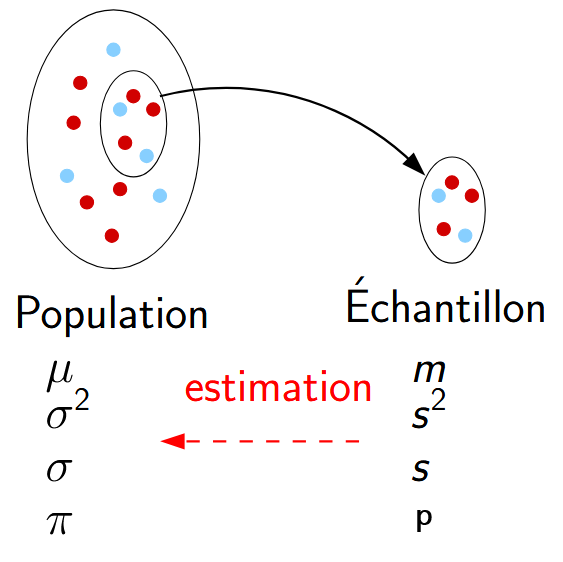
  • Echantilon de taille \(n\)

  • Paramètres dans la population : Inconnus

  • Paramètres dans l’échantillon : Connues

  • Objectif : estimer les paramètres dans la population

  • Deux types d’estimations :

    • Estimation ponctuelle
    • Intervalles de confiance :
      • moyenne
        • \(\sigma\) connu
        • \(\sigma\) inconnu
      • proportion


Estimation ponctuelle

  • \(\mu = m\)

  • \(\pi = p\)

  • \(\sigma = \sqrt{\dfrac{n}{n-1}} \ s\)

Exemple :

  • L’association MaCLoc distribue des paniers de légumes chaque semaine depuis plusieurs années.

  • On suppose que la variable aléatoire \(X\) qui, à chaque panier tiré au hasard, associe son poids, suit une loi normale.

  • Soucieux de l’equité pour les adhérents, on prélève un échantillon de 50 paniers à intervalle régulier. La moyenne s’élève à \(450 ~g\) et son écart-type à \(40 ~g\).

Question

Donner une estimation ponctuelle du poids moyen et de l’écart type des paniers distribués fabriqués par l’association MaCLoc.


Solution

cf. correction manuscrite


Intervalle de confiance

Pour une moyenne

  • Situation A : \(\sigma\) connu

L’intervalle de confiance vaut :

\[\left[m - t \ \dfrac{\sigma}{\sqrt{n}} \ ; \ m + t \ \dfrac{\sigma}{\sqrt{n}} \right]\]

  • Situation B : \(\sigma\) inconnu

L’intervalle de confiance vaut :

\[\left[m - t \ \dfrac{\sigma}{\sqrt{n}} \ ; \ m + t \ \dfrac{\sigma}{\sqrt{n}} \right]\]

où \(\sigma\) est cette fois une valeur estimée (ponctuelle) à partir de l’échantillon

Pour une proportion : Situation C

L’intervalle de confiance vaut :

\[\left[p - t \ \sqrt{\dfrac{p(1-p)}{n}} \ ; \ p + t \ \sqrt{\dfrac{p(1-p)}{n}} \right]\]

Conditions :

  • \(np >5\)
  • \(n(1-p)>5\)
  • \(np(1-p)>5\)


Valeur de t pour un seuil de rsique donné

  • seuil de risque : \(\alpha\)
    souvent \(\alpha = 0.05 = 5 \%\)

  • seuil de confiance : \(1-\alpha\)
    souvent \(1- \alpha = 0.95 = 95 \%\)

  • \(t\) est défini (pour la loi normale) comme : \[P\left(-t<X<t\right) = 1 - \alpha\] On a donc \[\begin{align*} P\left(-t<X<t\right) = 1 - \alpha &\Longleftrightarrow 2 P\left(X<t\right) - 1 = 1 - \alpha \\ &\Longleftrightarrow 2 \Pi\left(t\right) - 1 = 1 - \alpha \\ &\Longleftrightarrow \Pi\left(t\right) = \frac{2 - \alpha}{2} \\ \end{align*}\] Lecture inverse sur la table de la loi normale !

  • Exemple :   Pour \(\alpha = 0.05\), on a \(\Pi\left(t\right) = 0.975\) donc \(t=1.96\).


Exemple A :

  • Toujours avec l’association MaCLoc qui distribue des paniers de légumes chaque semaine depuis plusieurs années.

  • On suppose que la variable aléatoire \(X\) qui, à chaque panier tiré au hasard, associe son poids, suit une loi normale de moyenne inconnue et d’écart-type de \(30 ~g\)

  • On constitue un échantillon de 100 paniers et on calcul sa moyenne qui s’élève à \(420 ~g\).

Question

Donner une estimation du poids moyen par intervalle de confiance, au seuil de confiance de \(95 \%\)


Solution

cf. correction manuscrite


Exemple B :

Un échantillon aléatoire de coopératives de coton a donné la série statistique suivante :

\(X_i\)
Chiffre d’affaires		 \(n_i\)
(Coopérative)
\([0 ; 4[\) 4
\([4 ; 8]\) 10
\([8 ; 12[\) 12
\([12 ; 16[\) 9
\([16 ; 20[\) 5

Questions

  • Donner une estimation ponctuelle de la moyenne et de l’écart-type de la population.

  • Donner une estimation du CA moyen par intervalle de confiance, au niveau de confiance de \(99 \%\).


Solution

cf. correction manuscrite


Exemple C :

Une étude sur l’utilisation de machine mécanisée est menée dans les exploitations agricole au Rwanda, ce afin d’estimer le taux d’utilisation.

L’étude d’un échantillon de 100 fermes choisies d’une manière aléatoire conclut à un taux de \(18 \%\).

Questions

Dans quel intervalle de confiance peut-on situer le taux d’utlisation dans les fermes au Rwanda, au seuil de risque de \(5 \%\) ?


Solution

cf. correction manuscrite

Tests statistiques

coming !

Analyse factorielle

coming !