Exercices de Niveau Avancé

Exercice 21 : Layout

Les données old faithful geyser ont été collectées dans le cadre d’une étude du temps d’attente entre deux éruptions et la durée des éruptions au sein du parc National de Yellowstone (USA). Ce jeu de données est disponible sous \(R\) et est nommé faithful (package datasets). Le seuil critique d’attente au delà duquel la probabilité que la prochaine éruption soit longue et forte est fixé à 63 .

Télécharger et visualiser le jeu de données (fonction plot( )), en affichant également la limite des 63 secondes.
Calculer un vecteur vec de 100000 points correspondant à la loi normale de moyenne \(m\) et d’écart type sd correspondant à la moyenne, et à l’écart type, des durées d’éruption.
Construire un histogramme de la durée d’éruption. Représenter l’histogramme en terme de densité plutã’t qu’en terme d’effectifs (axe Y). Ajouter un titre, nommer les axes et colorer les barres de l’histogramme en vert et les traits de l’histogramme en rouge. Augmenter la taille du pas de l’histogramme à 20 .
Ajouter la densité du vecteur de point vec à l’histogramme (Indice : lines(), density(). Que remarquez-vous ?
Afin de mieux apprehender la distribution des données, il est possible d’afficher plusieurs graphiques sur une m \(\tilde{A}^{\text {a }}\) me grille. L’objectif de cette partie est d’afficher le scatterplot de la question 1, et au dessus et sur la droite, les histogrammes des variables “eruption” et “waiting”, respectivement. Pour cela, nous utiliserons la fonction layout(). 5.1 Créer la matrice suivante :

layMat = matrix(c(2,0,1,3), ncol=2, byrow=TRUE)
layMat
## [,1] [,2]
## [1,] 2 0
## [2,] 1 3

Cette matrice permettra à la fonction layout d’afficher les prochains plot :

en bas à gauche
en haut à gauche
en bas à droite (n.b : le chiffre 0 indique qu’aucun plot ne pourra \(\tilde{\mathrm{A}}^{\text {a }}\) tre affiché dans cette zone) 5.2 Utiliser la fonction layout et la matrice layMat pour créer une grille d’affichage ayant les proportions suivantes, puis afficher le résultats (indice : layout.show()) :
première colonne : \(70 \%\) de la largeur totale
deuxième colonne : \(30 \%\) de la largeur totale
première ligne : \(30 \%\) de la largeur totale
deuxième ligne : \(70 \%\) de la largeur totale 5.3 Afficher sur ce layout les 3 graphiques suivants:
le scatter plot de la question 1
l’histogramme de la variable “eruption”
l’histogramme de la variable “waiting” (indice : pensez à mettre l’hitogramme à l’horizontal)

#1
data(faithful)
?faithful
plot(faithful$waiting, faithful$eruptions)
abline(v=63, col="red")
#2
vec = rnorm(100000, mean = mean(faithful$eruptions), sd = sd(faithful$eruptions))
#3
hist(faithful$eruptions, freq = FALSE, main = "Histogramme de la durée des eruptions", xlab = "Durée de
#4
lines(density(vec))
#5
#5.1
layMat = matrix(c(2,0,1,3), ncol=2, byrow=TRUE)
#5.2
layout(layMat, widths=c(0.7, 0.3), heights=c(0.3, 0.7 ))
layout.show(n=3)
    ## scatter plot
plot(faithful, xlim=range(faithful$eruptions), ylim=range(faithful$waiting))
xhist = hist(faithful$eruptions, plot=FALSE, breaks=20)
yhist = hist(faithful$waiting , plot=FALSE, breaks=20)
barplot(xhist$density, axes=FALSE, space=0)
barplot(yhist$density, axes=FALSE, space=0, horiz=TRUE)

Exercice 22: ah si j’étais riche !

Un ami vous propose le jeu suivant. On lance un dé. Si le résultat est 5 ou 6 , on gagne \(3 €\), si le résultat est 4 on gagne \(1 €\) et si c’est 3 ou moins on perd \(2.5 €\). Avant d’accepter la partie, vous essayez de simuler ce jeu, pour voir si vous avez des chances de vous enrichir.

Créer une fonction simul qui prend comme argument un entier compris entre 1 et 6 , et qui retourne la somme correspondante.
Créer un vecteur tirage, simulant le résultat de 1000 tirages de dés.
Afficher sur un graphique la simulation du jeu.

Conclusion?
#1
simul = function(i){
    res = NULL
    if (i <= 6 && i >= 1){
        res = switch(i, -2.5, -2.5, -2.5, 1, 3, 3)
    }
    else {
        warning("Un tirage de dès en peut donner qu'un chiffre entre 1 et 6")
    }
    return(res)
}
#2
tirage = sample(x = c(1:6),size = 1000, replace = TRUE )
#3
resultat = sapply(tirage, simul)
gain = cumsum(resultat)
plot(gain)

Exercice 23 : James Bond autour du monde

R contient de nombreux packages nous permettant de faire des représentations graphiques de toutes sortes. Certains packages permettent de faire des représentations spatiales (rgdal, sp, rgeos,cartography). Connu comme une boite à outil dédiée à la cartographie thématique, le package cartography est développé au sein de l’UMS RIATE (CNRS, CGET, Université Paris Diderot) par Nicolas Lambert et Timothée Giraud.

Commencez par installer le package cartograpgy disponible sur le CRAN (via l’utilitaire RStudio ou en ligne de commande).

Nous allons construire une carte dont l’objectif sera de montrer le nombre de fois où 007 s’est rendu dans chaque pays.

Pour cela, télécharger les données disponibles à l’adresse suivante : http://wukan.ums-riate.fr/bond/bondfiles. RData. Nous avons chargé 2 objets :

Le data frame BondVisits contient 2 colonnes, l’identifiant des pays (ISO2) et le nombre de visites (n).
La liste WorldCountries : cette liste est une SpatialPolygonsDataFrame (spdf) contenant la carte de tous les pays du monde.

Afficher la carte du monde grÃcce à la fonction plot, qui prend en argument des données au format spdf, avec l’arrière plan en gris. On voit que les marges de la figures sont trop grandes. Modifiez les pour maximiser l’espace pris par la map monde. Redessinez la map monde. Indice par() option mar
Ajouter les cercles proportionnels correspondant aux nombres de visites dans chaque pays de 007, avec la couleur de votre choix et des bords blanc. Modifier le titre de la légende de “n” à “Nombres de visites”.
On veut à présent représenter le nombres de visites par des couches de couleurs différentes plutôt que par des symboles proportionnels. Quelle fonction doit-on utiliser ? Appliquer la fonction aux données. Le résultat obtenu vous parait-il correct?
Regarder le contenu de l’objet WorldCountries@data. Construisez un nouveau dataframe contenant tous les pays et les nombres de visites (NA ou 0 si inconnu). Réessayez de créer le graphique de la question précédente. Indice : pour créer le nouveau dataframe, la fonction merge peut vous être utile

library(cartography)
load((url("http://wukan.ums-riate.fr/bond/bondfiles.RData")))
head(BondVisits)
plot(WorldCountries, bg="gray")
par(mar = c(0,0,1.2,0))
plot(WorldCountries, bg="gray")
propSymbolsLayer(spdf = WorldCountries, df = BondVisits, var="n", border="white", col="magenta3", legen
choroLayer(spdf = WorldCountries, df = BondVisits, var="n")
BondVisits2 = merge(BondVisits, WorldCountries@data, by="ISO2", all.y=TRUE)
choroLayer(spdf = WorldCountries, df = BondVisits2, var="n", legend.title.txt = "Nombre de visites")

Exercice 24 : Profil CGH

Les technologies de génomique permettent de détecter des abérrations au niveau de notre génome (CNA - Copy Number Alteration) : duplication, remaniement, translocation, perte, etc … En cancérologie, le génome des tumeurs est souvent anormal (voir la figure “Profil CGH”).

Cet exercice a pour objectif de reconstruire ce profil à partir du package “chromosomes” (développé par B. Job, Gustave Roussy) et du jeu de données A01.ASPCF, issu de l’analyse par des microarrays du type “Oncoscan” (Affymetrix) de la tumeur d’un patient.

Installer le package ‘chromosomes_1.0-0.tgz’ (ce fichier est récupérable sur le site du TP). Charger le package avec la commande library(); Enfin, charger le dataset hg19. Ceci importe dans votre session \(R\) une variable nommée cs (chromosome structure) décrivant les positions du génome humaine (version hg19).

Quelle est la classe de la variable cs ?
Combien le génome contient-il de chromosomes? (Indice : parcourir l’obet cs avec la fonction str)
Quelle est la taille du génome humain (dans sa version hg19) ?

Charger le fichier A01. ascat. ASPCF.RDS dans la variable cgh

Quelle est la classe de la variable cgh ?
Combien d’éléments contient cette variable ?
Quelle est le genre du patient à qui correspond le profil?

Construction du profil CNA

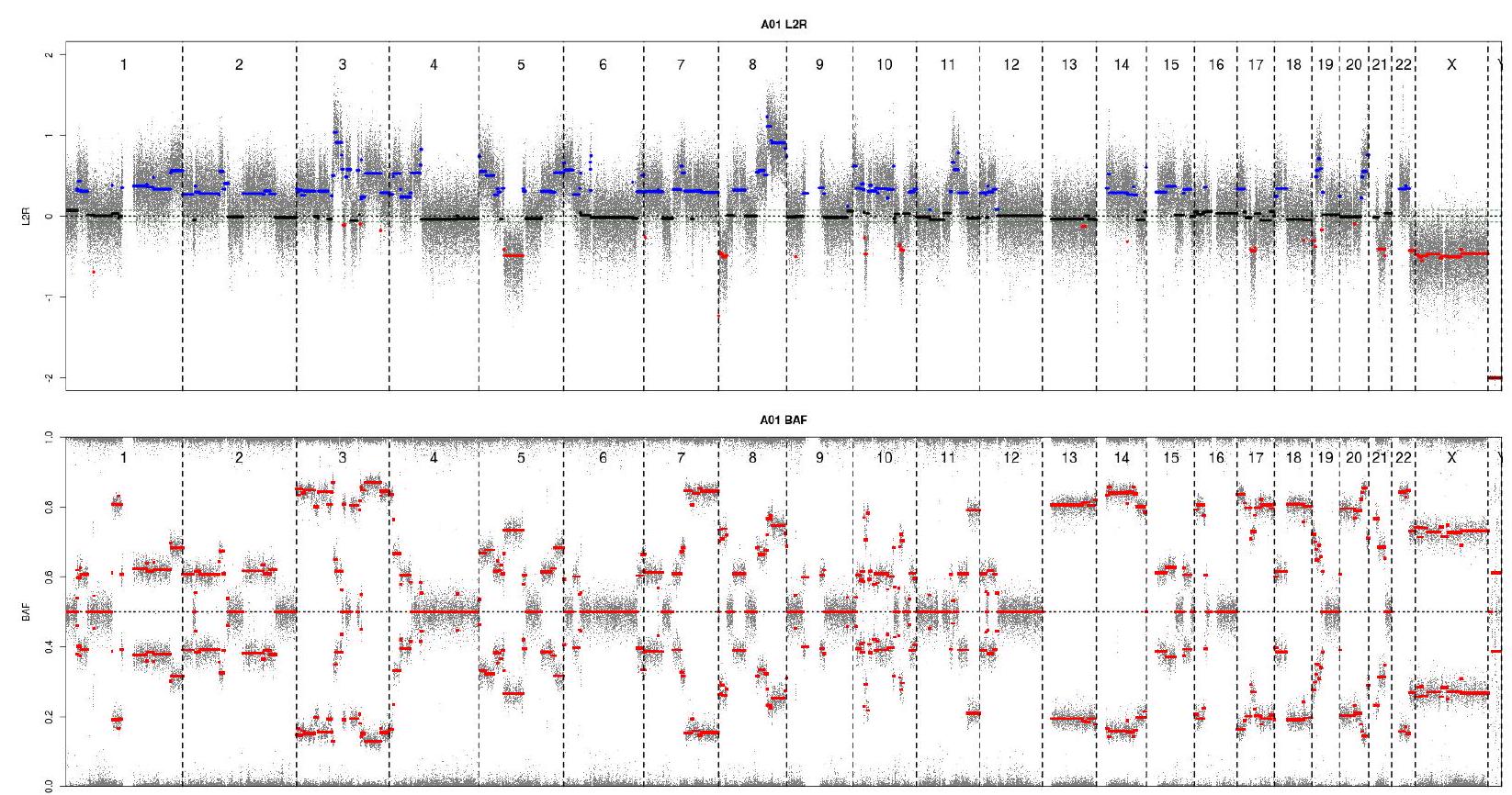
Figure 1: Profil CGH a. Construction des vecteurs de points à afficher depuis la variable cgh :

Créer le vecteur tumor_lr à partir de la variable cgh
Créer le vecteur x_snp contenant les positions génomique des points de mesure
Créer le vecteur x_chr contenant les nom des chromosomes auxquels appartiennent les points de mesure
Créer le vecteur all_chr contenant une seule occurrence de ces noms de chromosomes

En utilisant la variable cs, construisez le vecteur chr_length, contenant les longueurs des chromosomes. Utiliser la fonction names et la variable cs pour nommer tous les éléments du vecteur chr_length.
Convertir les positions relatives au chromosome du vecteur \(x_{-}\)snp en position absolue sur le génome (vecteur x_snp_abs)
Afin d’afficher une version lissée du signal mesuré, calculer la “running médiane” (Indice : fonction runmed) à partir du vecteur l2r_tumor
A partir de ces vecteurs, essayez de reproduire l’image suivante.

Indice: les lignes vertes correspondent à la moyenne des valeurs absolues des différences mesurées entre deux sondes

#1
install.packages("chromosomes_1.0-0.tar.gz", repos = NULL, type = "source")
library("chromosomes")
data(hg19)
#1.1
class(cs)
#1.2
str(cs)
length(cs$chromosomes$chrom)

Figure 2: Ebauche de Profil CGH

#1.3
str(cs)
cs$genome.length
#2
cgh = readRDS(file = "data/A01.ascat.ASPCF.RDS")
#2.1
class(cgh)
#2.2
length(cgh)
#2.3
cgh$gender
#3.1
y_tumor_12r = cgh$Tumor_LogR[,1]
x_snp = as.numeric(as.vector(cgh$SNPpos$pos))
x_chr = as.vector(cgh$SNPpos$chrs)
all_chr = unique(x_chr)
#3.2
chr_length = cs$chromosomes$chr.length.toadd
chr_names = cs$chromosomes$chrN
names(chr_length) = chr_names
#3.3
x_snp_abs = x_snp
for (i in all_chr){
    idx = which(x_chr == i)
    if (i == "X") { tmp.chr = 23}
    else if (i == "Y") { tmp.chr = 24}
    else { tmp.chr = as.numeric(i)}
    valtoadd = chr_length[tmp.chr]

    x_snp_abs[idx] = x_snp_abs[idx] + valtoadd
}
#3.4
l2r_runmed = runmed(y_tumor_l2r , k = 301)
#3.5
plot(x_snp_abs, y_tumor_l2r, ylim = c(-2, 2),col = "gray", pch = ".", ylab = "Log2R", xlab = "", axes =
axis(2)
points(x_snp_abs, l2r_runmed, col="blue", pch = ".")
abline(h = 0, lty = 2, col = "red")
abline(v = c(0,cs$chromosomes$chr.length.sum), lty = 2, col = "black")
box(lwd = 2)
tmp = mean(abs(diff(y_tumor_12r)))
abline(h = c(-tmp, tmp), lty = 2, col = "darkgreen")
pair = seq(from = 2, to = 24, by = 2)
impair = seq(from = 1, to = 23, by = 2)
text(x = cs$chromosomes$mid.chr[pair] + cs$chromosomes$chr.length.toadd[pair], y = 1.7 , labels = a
text(x = cs$chromosomes$mid.chr[impair] + cs$chromosomes$chr.length.toadd[impair], y = -1.7, labels = a