x = c(22.03,50.60,14.43,4.01,7.90,1.03)
NamesNav <- c("Chrome","Firefox","Internet Explorer","Opera","Safari","Autres")
barplot(x,col=c(1,2,3),border=NA,names.arg=NamesNav)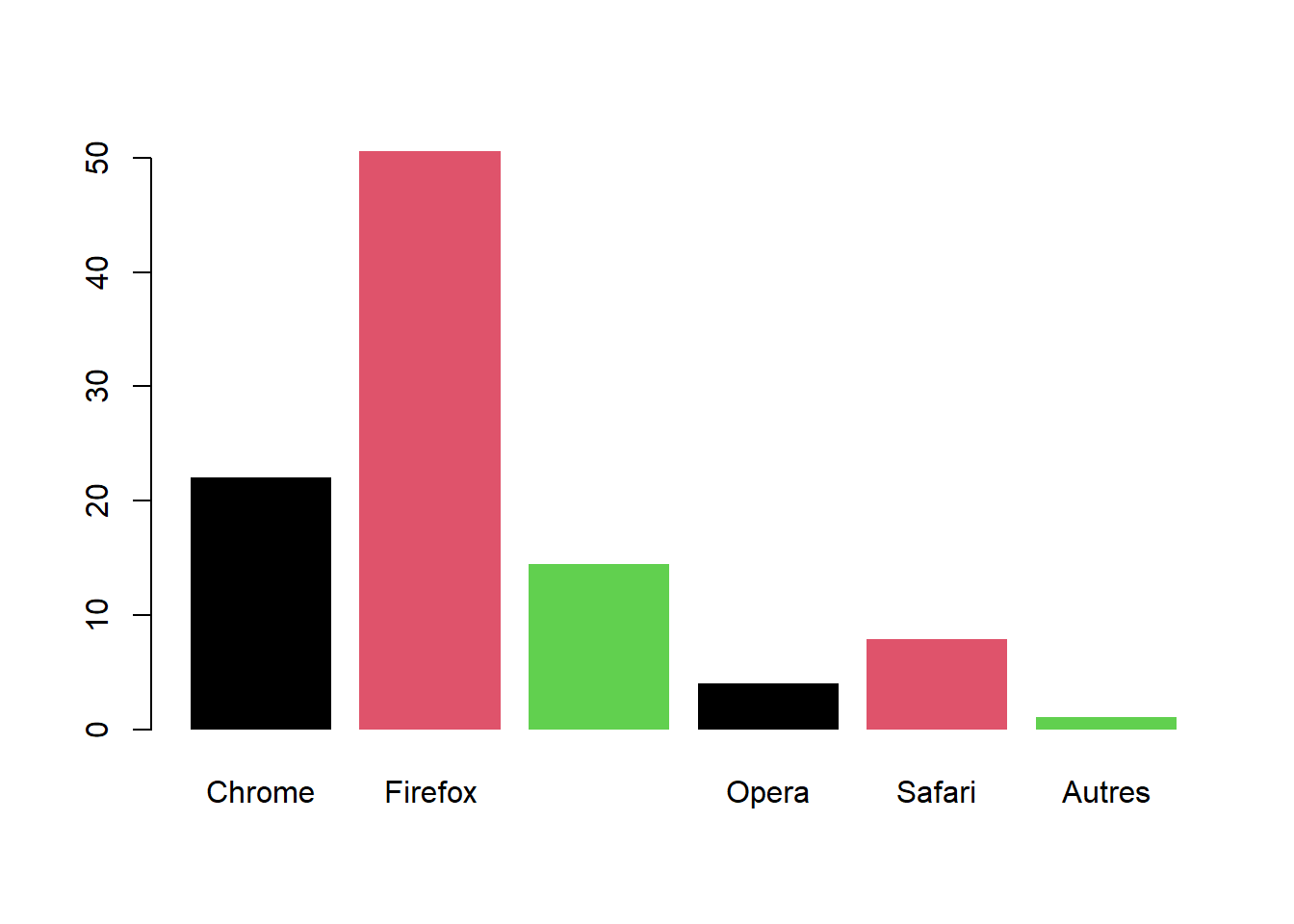 
Exercices
Statistiques univariées
Variables Qualitatives
Exercice 1.1
Le nombre de visites classé par le navigateur internet utilisé pour accéder au site internet de l’ISTOM le moi dernier est donné dans le tableau suivant.
| Navigateur (\(x_i\)) | Nombre de visites (\(n_i\)) |
|---|---|
| Chrome | 880491 |
| Firefox | 2022764 |
| Internet Explorer | 576655 |
| Opera | 160303 |
| Safari | 315613 |
| Autres | 41367 |
Déterminer la population (en précisant sa taille et les individus qui la compose), les variables étudiées, leur type et les modalités qu’elles prennent.
Déterminer la distribution des proportions de la variable «navigateur utilisé».
Quel est le mode de la variable ?
Représenter graphiquement la distribution des proportions.
Correction Ex. 1.1
- Population : visites d’un site dédié à l’informatique durant le mois de mars 2011.
- Individu : une de ces visites
- Effectif total : 2 022 764 + 880 491 + 576 655 + 315 613 + 150 639 + 51 031 = 3 997 193.
- Variables étudiées : une seule variable, le navigateur utilisé lors de la visite. C’est une variable qualitative nominale qui prend les six modalités «Firefox», «Chrome», «Internet Explorer», «Safari », «Opera» et «Autres».
- Voici le tableau de distribution des effectifs et des proportions :
| Navigateur | Effectif | Proportion |
|---|---|---|
| Chrome | 880491 | \(22,03 \%\) |
| Firefox | 2022764 | \(50,60 \%\) |
| Internet Explorer | 576655 | \(14,43 \%\) |
| Opera | 160303 | \(4,01 \%\) |
| Safari | 315613 | \(7,90 \%\) |
| Autres | 41367 | \(1,03 \%\) |
| 3997193 | \(100 \%\) |
Le mode est la modalité dont l’effectif est le plus grand, c’est-à-dire « Firefox ».
Puisque la variable est qualitative, on utilise un diagramme en baton :
[stat-1000]
Variable Quantitative Discrètes
Exercice 2.1
Pour un exerice de PIDEx, un groupe d’étudiant-es releve le nombre de piments sur chaque planche de culture d’une exploitation agricole. Les donnée brutes sont les suivantes :
12, 6, 8, 3, 15, 4, 8, 9, 10, 5, 6, 12, 8, 10
Déterminer la population (en précisant sa taille et les individus qui la compose), les variables étudiées, leur type et les modalités qu’elles prennent.
Déterminer la distribution des proportions de la variable «nombre de piments».
Représenter graphiquement la distribution des proportions.
Déterminer le mode de la variable.
Déterminer la moyenne de la variable.
Déterminer l’écart-type de la variable.
Déterminer la médiane de la variable à partir des données individuelles.
Correction Ex. 2.1
- Population : les planches de piments
- Individu : une de ces planches
- Effectif total : 14
- Variables étudiées : une seule variable, le nombre de piment par planche. C’est une variable quantitative discrète qui prend les neuf modalités \(3,4,5,6,8,9,10,12,15\).
- Voici le tableau de distribution des effectifs et des proportions.
| Note | Effectif | Proportion |
|---|---|---|
| 3 | 1 | \(7,14 \%\) |
| 4 | 1 | \(7,14 \%\) |
| 5 | 1 | \(7,14 \%\) |
| 6 | 2 | \(14,29 \%\) |
| 8 | 3 | \(21,43 \%\) |
| 9 | 1 | \(7,14 \%\) |
| 10 | 2 | \(14,29 \%\) |
| 12 | 2 | \(14,29 \%\) |
| 15 | 1 | \(7,14 \%\) |
| TOTAL | 14 |
- Puisque la variable est quantitative discrète, on utilise un diagramme en bâtons :
y = c(0,0,0,7.14,7.14,7.14,14.29,0,21.43,7.14,14.29,14.29,0,0,7.14,0,0,0)
z = c(0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17)
barplot(y,col="steelblue",names.arg=z)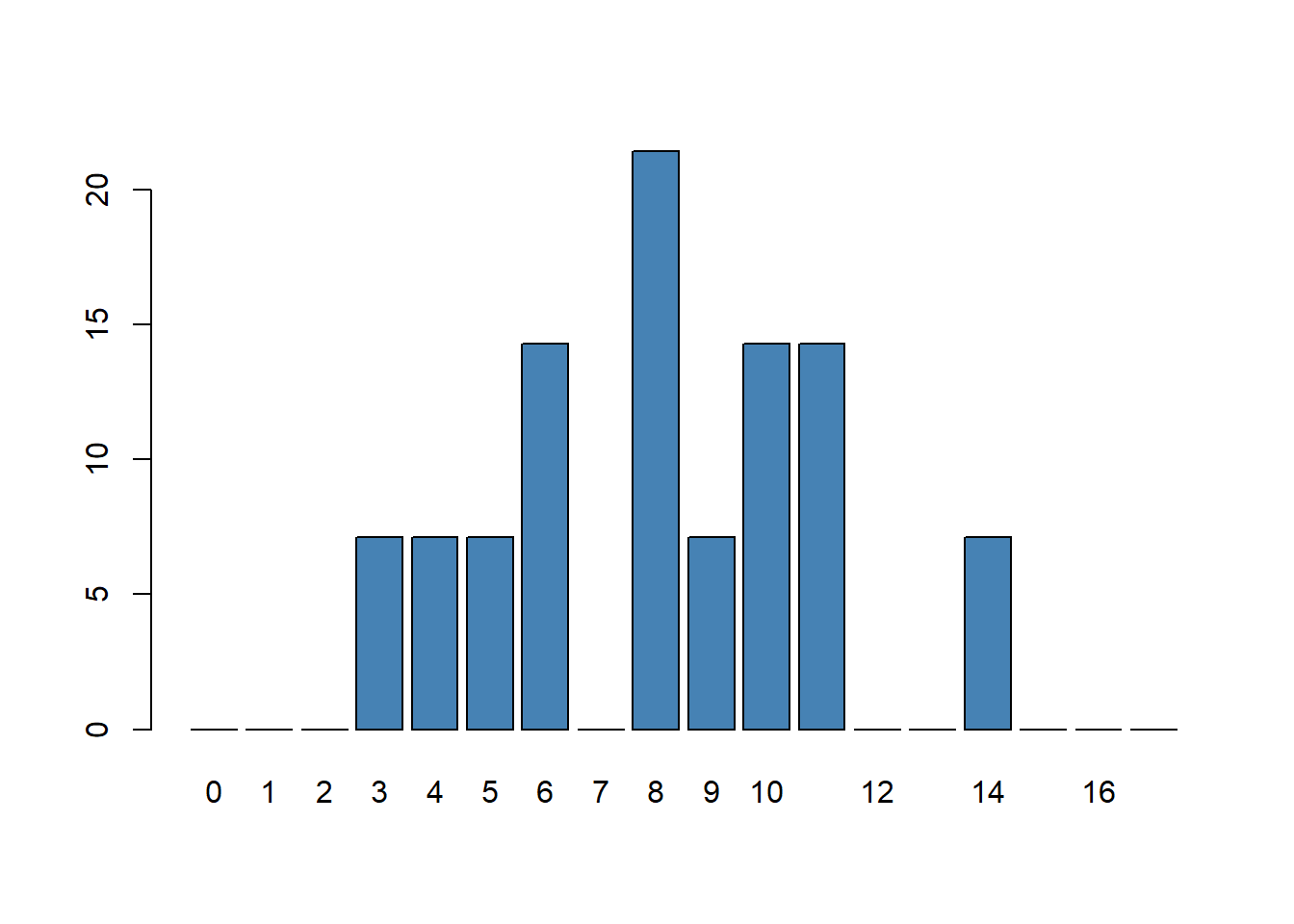
Le mode est la modalité dont l’effectif est le plus grand, c’est-à-dire «8».
Pour calculer la moyenne on utilise la formule suivante :
\[ \begin{aligned} \mu & =\frac{\sum_{i=1}^{k} n_{i} x_{i}}{N} \\ & =\frac{1 \times 3+1 \times 4+1 \times 5+2 \times 6+3 \times 8+1 \times 9+2 \times 10+2 \times 12+1 \times 15}{14} \\ & =\frac{116}{14} \\ \mu &\simeq 8,2857 \end{aligned} \]
- Pour calculer l’écart-type on utilise la formule suivante :
\[\sigma =\sqrt{\frac{\displaystyle\sum_{i=1}^{k} n_{i} x_{i}^{2}}{N}-\mu^{2}}\] Avec \[\sum_{i=1}^{k} n_{i} x_{i}^{2} = 1 \times 3^{2}+1 \times 4^{2}+1 \times 5^{2}+2 \times 6^{2}+3 \times 8^{2}+1 \times 9^{2}+2 \times 10^{2}+2 \times 12^{2}+1 \times 15^{2} = 1108\] Donc \[\sigma = \sqrt{\frac{1108}{14}-8,2857^{2}} \simeq 3,2388 \]
- Puisque l’effectif total \(N\) est pair, pour déterminer la médiane à partir des données individuelles, on les range par ordre croissant et on fait la moyenne des deux valeurs du milieu :
\[ 3,4,5,6,6,8,8, \mid 8,9,10,10,12,12,15 \]
Les deux valeurs du milieu (de part et d’autre du trait) sont 8 et 8 donc la médiane est \(\dfrac{8+8}{2}=8\).
[stat-1001]
Exercice 2.2
Un étudiant en stage de fin d’étude fait un contrôle de qualité sur des parcelles de goyaviers. Il souhaite évaluer l’importance de la production en goyave sur chacune des parcelle. Pour cela il atribue une note sur 5 pour chaque goyavier de chaque parcelle. La noté de 0 étant un goyavier sans aucun fruit, et 5 un abondant de fruits. Les parcelles sont notée A, B, C et D.
Pour chacune des parcelle déterminer la médiane à partir du tableau de distribution des effectifs.
| Note | Effectif Parcelle A | Effectif Parcelle B | Effectif Parcelle C | Effectif Parcelle D |
|---|---|---|---|---|
| 0 | 3 | 3 | 3 | 3 |
| 1 | 5 | 3 | 3 | 3 |
| 2 | 8 | 3 | 3 | 3 |
| 3 | 6 | 3 | 3 | 3 |
| 4 | 2 | 3 | 3 | 3 |
| 5 | 1 | 3 | 3 | 3 |
Correction Ex. 2.2
coming.
Variable Quantitatives Continues
Exercice 3.1
La répartition des étudiant-es cette année selon la durée de trajet (en minute) pour se rendre à l’ISTOM est donné par le tableau statistique ci-dessous.
Tableau statistique
| \([e_i,e_{i+1}[\) | \(f_i\) | \(F_i\) | \(p_i\) | \(P_i\) | \(a_i\) | \(c_i\) | \(d_i\) |
|---|---|---|---|---|---|---|---|
| [0,5[ | 0.0285 | ||||||
| [5,10[ | 0.0996 | ||||||
| [10,15[ | 0.1358 | ||||||
| [15,20[ | 0.1286 | ||||||
| [20,25[ | 0.1141 | ||||||
| [25,30[ | 0.0947 | ||||||
| [30,40[ | 0.1361 | ||||||
| [40,50[ | 0.0815 | ||||||
| [50,70[ | 0.0796 | ||||||
| [70,120[ | 0.1015 |
avec \(d_i\) la fréquence relative. La durée de trajet maximale a été arbitrairement choisie à 120 min pour les besoins de l’exercice.
Déterminer la population et la variables étudiée (en précisant son type).
Représenter graphiquement la distribution des proportions.
Déterminer la classe modale de la variable.
Représenter graphiquement la proportion des étudiant-es ayant un trajet compris entre 7 et 22 minutes. Calculer cette proportion.
Calculer, à l’aide de la fonction de répartition, la proportion d’étudiant-es mettant moins de 35 minutes pour venir à l’école. Même question pour un temps de trajet compris entre 17 et 35 minutes.
Déterminer la moyenne et l’écart-type de la variable.
Déterminer la médiane, les quartiles ainsi que les premier et neuvièmes déciles.
Représenter graphiquement la fonction de répartition.
Correction Ex. 3.1
coming.
Exercice 3.2
Le temps de trajet domicile - lieu de la pratique sportive (en minutes) déclaré par les étudiant-es istomiens a été récolté. On a commencé à remplir le tableau statistique suivant.
Tableau statistique
| \([e_i,e_{i+1}[\) | \(f_i\) | \(F_i\) | \(p_i\) | \(P_i\) | \(a_i\) | \(c_i\) | \(d_i\) |
|---|---|---|---|---|---|---|---|
| [0,5[ | 0.0337 | ||||||
| [5,10[ | 0.144 | ||||||
| [10,15[ | 0.294 | ||||||
| [15,20[ | 0.4522 | ||||||
| [20,25[ | 0.5971 | ||||||
| [25,30[ | 0.655 | ||||||
| [30,35[ | 0.7869 | ||||||
| [35,45[ | 0.846 | ||||||
| [45,60[ | 0.9201 | ||||||
| [60,90[ | 0.9722 | ||||||
| [90,150[ | 1 |
Représenter la boîte à moustache.
Déterminer l’intervalle de variation à \(75 \%\).
Déterminer l’intervalle de variation à \(95 \%\).
Correction Ex. 3.2
coming.
Statistiques bivariées
Qualitative - Qualitative
Exercice 4.1
Un site internet reçoit 113457 visiteurs durant un mois. On désigne par \(X\) le navigateur internet utilisé et \(Y\) le système d’exploitation utilisé.
| Windows | Mac | Linux | |
|---|---|---|---|
| Chrome | 14103 | 1186 | 427 |
| Firefox | 30853 | 4392 | 3234 |
| Internet Explorer | 47389 | 23 | 0 |
| Safari | 668 | 6416 | 0 |
| Autres | 2974 | 40 | 1752 |
Identifier la population, sa taille ainsi que les variables étudiées en précisant leur type.
Quelle est la proportion de visiteurs sous Windows?
Quelle proportion de visiteurs utilisent le navigateur Safari?
Parmi les utilisateurs de Mac, quelle proportion utilise Chrome?
Parmi les utilisateurs de Safari, quelle proportion est sous Windows?
Représenter graphiquement la distribution des proportions par Navigateur pour chaque système d’exploitation. Les variables \(X\) et \(Y\) sont-elles indépendantes?
[stat-0001]
Qualitative - Quantitative
Exercice 5.1
Influence d’un incinérateur sur le taux de métaux lourds dans l’air.
Dans le tableau ci-dessous, sont relevées les valeurs du taux de plomb (en ng/m \({ }^3\) ) dans l’air pour trois stations ORAMIP de Toulouse : Eisenhower et Chapitre, qui sont situées à proximité de l’incinérateur de déchets du Mirail, et Berthelot, situé en zone urbaine, qui est caractéristique de l’air respiré par l’ensemble de la population toulousaine.
| Eisenhower | Chapitre | Berthelot |
|---|---|---|
| 7,6 | 9,1 | 7,5 |
| 21,4 | 13,1 | 9,3 |
| 12,4 | 10,5 | 10,2 |
| 15,8 | 8,3 | 20,3 |
| 14,8 | 17,4 | 10,3 |
| 5,9 | 9,4 | 16,4 |
| 12,5 | 7,8 | 13,3 |
| 11,3 | 12,2 | 14,9 |
On considère ici la population des relevés de taux de plomb de taille 24 et les variables X (Taux de plomb dans l’air), et Y (Station).
De quels types sont les variables considérées?
Sur cet échantillon de relevés, peut-on considérer qu’il y a un lien important entre la station de relevé et le taux de plomb dans l’air?
Si on considère maintenant la variable Z (Proximité de l’incinérateur), de type qualitative nominale, peut-on considérer qu’il y a un lien important entre X et Z ?
Quantitative - Quantitative
Exercice 6.1
En 1885, Francis Galton publie un tableau de données comparant la taille \(Y\) des enfants avec la taille \(X\) de leurs parents (la taille des parents est égale à la moyenne de la taille du père et de la mère). Pour compenser les différences de tailles entre sexes, toutes les tailles des personnes de sexe féminin ont été multiplié par 1,08. Les tailles sont exprimées en pouces \((1\) pouce \(=2,54 \mathrm{~cm})\).
| X Y | ]60;61,7] | ]61,7;63,7] | ]63,7;65,7] | ]65,7;67,7] | ]67,7;69,7] | ]69,7;71,7] | ]71,7;73,7] | 173,7;75] |
|---|---|---|---|---|---|---|---|---|
| ]62;64] | 1 | 2 | 5 | 4 | 2 | 0 | 0 | 0 |
| ]64;66] | 2 | 14 | 17 | 32 | 16 | 7 | 1 | 0 |
| ]66;68] | 0 | 14 | 36 | 108 | 93 | 34 | 4 | 0 |
| ]68;70] | 1 | 8 | 47 | 100 | 135 | 84 | 22 | 5 |
| ]70;72] | 1 | 1 | 2 | 11 | 38 | 35 | 18 | 5 |
| ]72;74] | 0 | 0 | 0 | 0 | 3 | 3 | 13 | 4 |
Les bornes des classes extrêmes ont été fixées arbitrairement pour les besoins de l’exercice.
Préciser la population, les individus, la taille de la population ainsi que les variables étudiées.
Quelle est la proportion d’enfants dont la taille est comprise entre 65,7 et 67,7?
Parmi les enfants dont la taille est comprise entre 71,7 et 73,7, quelle proportion a des parents dont la taille est entre 70 et 72 ?
Quelle est la taille moyenne des enfants dont les parents ont une taille comprise entre 68 et 70 ? Convertir le résultat en centimètres.
Même question pour la taille médiane.
Même question pour l’écart-type.
Exercice 6.2 (Corrélation et causalité)
Une bonne corrélation entre deux séries de données ne signifie pas pour autant qu’il existe un lien de cause à effet entre les deux. Pour illsutrer cette affirmation, considérons la série statistique suivante :
| Année | 1996 | 1997 | 1998 | 1999 | 2000 |
|---|---|---|---|---|---|
| Morts | 15.85 | 15.7 | 15.39 | 15.32 | 14.85 |
| Importations de citrons | 230 | 280 | 360 | 410 | 525 |
Ce tableau donne le nombre de morts (pour un million d’habitants) sur les autoroutes américaines, ainsi que le nombre de tonnes de citrons mexicains importés aux États-Unis de 1996 à 2000.
Calculer le coefficient de corrélation linéaire pour cette série double. En déduisez vous une information pertinente ?
Remarque
Attention donc à l’erreur courante qui est de croire qu’un coefficient de corrélation linéaire élevé (en valeur absolue) induit une relation de causalité entre les deux phénomènes mesurés.