Examen de statistiques et analyse de données

Auteur·rice
Affiliation

Antoine Géré

Promotion 114

Date de publication

10 décembre 2025

Exercice 1

Le coucou européen ne couve pas ses propres oeufs, mais les dépose dans les nids d’oiseaux d’autres espèces. Des études antérieures ont montré que les coucous ont parfois évolué pour pondre des oeufs dont la couleur est similaire à celle des oeufs de l’espèce hôte.

Est-ce également le cas pour la taille des oeufs ? Les coucous pondent-ils des oeufs de taille similaire à ceux de leurs hôtes ?

Le fichier de données est cuckooeggs.csv

cuckooeggs = read.csv("data_raw/cuckooeggs.csv")
head(cuckooeggs)
   host_species egg_length
1 Hedge Sparrow      20.85
2 Hedge Sparrow      21.65
3 Hedge Sparrow      22.05
4 Hedge Sparrow      22.85
5 Hedge Sparrow      23.05
6 Hedge Sparrow      23.05
summary(cuckooeggs)
 host_species         egg_length   
 Length:120         Min.   :19.65  
 Class :character   1st Qu.:21.85  
 Mode  :character   Median :22.35  
                    Mean   :22.46  
                    3rd Qu.:23.25  
                    Max.   :25.05
1. Le fichier de données

Présentez le fichier de données en indiquant le nombre de variables, leur type ainsi que leurs principales caractéristiques.

Le jeu de données cuckooeggs contient :

  • 120 observations (lignes)

  • 2 variables :

Variable Type Description
host_species qualitative (facteur) Espèce hôte où le coucou a pondu
egg_length quantitative continue Longueur de l’œuf (en mm)
  • Caractéristiques principales de host_species :
    • 6 modalités :
      • Hedge Sparrow
      • Meadow Pipit
      • Pied Wagtail
      • Robin
      • Tree Pipit
      • Wren
  • Caractéristiques principales de egg_length :
    • minimum : 19.65 mm
    • maximum : 25.05 mm
    • moyenne : 22.46 mm
    • médiane : 22.35 mm

Les données sont adaptées à une analyse comparative de moyennes entre groupes.

Nous traçons quelques graphiques ci-dessous.

library(ggplot2)
ggplot(cuckooeggs, aes(x = egg_length)) +
geom_histogram(bins = 10, fill = "lightblue", color = "black") +
facet_wrap(~ host_species, scales = "free_y") +
labs(
title = "",
x = "Longueur (mm)", y = "Fréquence"
)

2. Interprétation des graphes ci-dessus
  1. Comment se nomme ce type de graphe ?
  2. Décrivez les différences visibles entre les distributions des longueurs d’oeufs selon les espèces hôtes.
  3. Les variances semblent-elles comparables ?
  4. Les distributions paraissent-elles approximativement normales ?
  5. Les moyennes semblent-elles clairement différentes ?

Il s’agit d’un ensemble d’histogrammes, un pour chaque espère hôte.

  • L’axe des abscisses représente des classes de valeurs de la longueur des œufs (en millimètres)

  • L’axe des ordonnées représente la fréquence (nombre d’observations par classe)

  • Contrairement à un diagramme en baton, les classes sont continues, ce qui est caractéristique des histogrammes

  • Différences de position (centre de la distribution)

    • On observe que les histogrammes ne sont pas centrés au même endroit.

    • Les distributions associées à Hedge Sparrow et Tree Pipit sont centrées autour de valeurs relativement élevées (autour de 23 mm).

    • À l’inverse, la distribution correspondant à Wren est clairement décalée vers la gauche, avec des valeurs majoritairement comprises entre 20 et 22 mm.

    • Les espèces Meadow Pipit, Pied Wagtail et Robin occupent une position intermédiaire.

    • Cela suggère que la taille moyenne des œufs varie selon l’espèce hôte.

  • Différences de dispersion (étalement des distributions)

    • Certaines espèces présentent une distribution plus concentrée (barres regroupées sur un intervalle étroit). D’autres montrent un étalement légèrement plus large, traduisant une plus grande variabilité.

    • Aucun histogramme ne montre cependant une dispersion extrêmement plus grande ou plus petite que les autres. Les largeurs des distributions restent globalement comparables. Cela suggère que les variances entre groupes sont relativement proches, sans hétérogénéité flagrante.

  • Différences de forme

    • Toutes les distributions semblent unimodales (un seul pic principal).

    • Les formes sont globalement symétriques, ou très légèrement asymétriques.

    • Aucune distribution ne présente de bimodalité (deux pics), ou de valeurs “aberrantes” clairement visibles.

  • On observe que Hedge Sparrow et Tree Pipit présentent des plages de valeurs très proches. En revanche, la distribution de Wren chevauche moins celles des autres espèces. Cela suggère que toutes les différences ne seront pas nécessairement significatives, mais que certaines espèces (notamment Wren) pourraient se distinguer nettement.

Les variances semblent comparables. En effet :

  • L’étendue des valeurs (distance entre minimum et maximum) est similaire entre espèces.

  • La largeur des histogrammes (nombre de classes occupées) ne varie pas fortement.

  • Aucun groupe ne montre une dispersion particulièrement élevée ou faible.

  • Ces observations suggèrent une homogénéité des variances, condition importante pour l’ANOVA. Cependant une simple observation graphique ne permet pas de conclure définitivement, mais elle constitue une première validation qualitative avant un test, comme le test de Levene.

Les distributions paraissent approximativement normales, en effet :

  • Les histogrammes ont une forme globalement en cloche.

  • La majorité des observations se situe autour d’une valeur centrale.

  • Les fréquences diminuent progressivement lorsqu’on s’éloigne du centre.

  • Les “queues” gauche et droite ne semblent ni très longues ni très asymétriques.

  • Même si la normalité n’est pas parfaite (ce qui est courant en données biologiques), les distributions semblent compatibles avec une hypothèse de normalité approximative. La normalité requise pour certains test, comme l’ANOVA, concerne surtout les résidus du modèle, et non nécessairement chaque groupe pris séparément.

Les moyennes semblent différentes, mais pas toutes de manière évidente. En effet :

  • La moyenne de Wren apparaît nettement plus faible que celles des autres espèces.

  • Les moyennes de Hedge Sparrow, Tree Pipit et Pied Wagtail semblent proches les unes des autres.

  • Certaines différences sont legeres et difficiles à quantifier visuellement.

  • On peut donc conclure qu’il existe des indices visuels de différences de moyennes, mais que l’ampleur de ces différences ne peut être évaluée précisément sans un test statistique.

On demande à R de nous donner les moyennes et les écarts types de la longueur des oeufs pour chacune des espèces hotes.

stats <- cuckooeggs %>%
group_by(host_species) %>%
summarise(
Moyenne = mean(egg_length),
Ecart_type = sd(egg_length),
n = n()
)
stats
# A tibble: 6 × 4
  host_species  Moyenne Ecart_type     n
  <chr>           <dbl>      <dbl> <int>
1 Hedge Sparrow    23.1      1.07     14
2 Meadow Pipit     22.3      0.921    45
3 Pied Wagtail     22.9      1.07     15
4 Robin            22.6      0.685    16
5 Tree Pipit       23.1      0.901    15
6 Wren             21.1      0.744    15
3. Interprétation du tableau descriptif
  1. Quelle espèce hôte présente les œufs les plus grands en moyenne ?
  2. Quelle espèce présente les œufs les plus petits en moyenne ?
  3. Les différences de moyennes vous semblent-elles importantes ?
  4. Les écarts-types semblent-ils homogènes ?

Le tableau présenté résume, pour chaque espèce hôte, des statistiques descriptives essentielles de la longueur des œufs de coucou (la moyenne, l’écart-type et la taille d’échantillon). Ces statistiques permettent de :

  • comparer la tendance centrale entre groupes,

  • évaluer la variabilité intra-groupe,

  • apprécier la fiabilité des estimations (via les tailles d’échantillon).

Les espèces qui présentent les plus grandes longueurs moyennes d’œufs sont Hedge Sparrow et Tree Pipit avec en moyenne des longueurs de 23,1 mm.

L’espèce qui présentent les œufs les plus petits en moyenne est Wren avec en moyenne des longueurs de 21,1 mm. Cette moyenne est nettement inférieure à celle de toutes les autres espèces. L’écart avec les espèces aux plus grandes moyennes est d’environ 2 mm, ce qui est substantiel à l’échelle de la longueur totale d’un œuf (10 %). Cela indique que les œufs pondus dans les nids de Wren sont significativement plus petits.

L’écart maximal observé entre espèces est \[23,1 ~\mbox{ mm } \ − \ 21,1 ~\mbox{ mm } \ = \ 2,0 ~\mbox{ mm }\]

Cet écart représente environ 9 % de la longueur moyenne d’un œuf, ce qui n’est pas négligeable. Les écarts-types sont de l’ordre de 0,7 à 1,1 mm. Un écart de 2 mm correspond donc à environ 2 à 3 écarts-types. Une différence de cette importance est potentiellement statistiquement significative.

Les valeurs observées sont :

Espèce Écart-type
Hedge Sparrow 1,07
Meadow Pipit 0,92
Pied Wagtail 1,07
Robin 0,69
Tree Pipit 0,90
Wren 0,74

Tous les écarts-types sont compris entre 0,69 et 1,07 mm. Le rapport entre le plus grand et le plus petit écart-type est :

\[\frac{1,07}{0,69} \approx 1,55 \]

En pratique, un ratio inférieur à 2 est souvent considéré comme acceptable. Aucune espèce ne présente une variabilité particulièrement élevée. Les dispersions sont comparables, même si elles ne sont pas strictement identiques. On peut donc raisonnablement supposer une homogénéité des variances, condition essentielle différents test comme l’ANOVA.

L’homogénéité des variances n’exige pas une égalité parfaite, mais une similarité raisonnable des dispersions entre groupes.

On se propose, afin de savoir si les coucous pondent des oeufs de tailles différentes selon l’espèce hôte, de réaliser un T-test.

t.test(egg_length ~ host_species, data = cuckooeggs)

4. Interprétation d’une erreur

Expliquez la raison pour laquelle ce t.test ne fonctionne pas dans ce cas précis.

Le t-test de Student est un test paramétrique destiné à comparer la moyenne d’une variable quantitative entre deux groupes. Il existe plusieurs variantes :

  • t.test à un échantillon

  • t.test pour échantillons indépendants (2 groupes)

  • t.test apparié

Dans tous les cas, le t-test est conçu pour comparer exactement deux groupes. Or dans notre étude :

  • Variable dépendante : egg_length (quantitative continue) \(\to\) possède 6 modalités distinctes !

  • Variable explicative : host_species (qualitative nominale)

Le modèle demandé par egg_length ~ host_species implique donc une comparaison entre 6 groupes !

Le t-test calcule une statistique t basée sur la différence entre deux moyennes et compare cette différence à la variabilité intra-groupe. Avec plus de deux groupes il n’existe pas de différence unique à tester. Il faudrait comparer toutes les paires possibles. Dans notre cas : \[\binom{6}{2}=15 \text { comparaisons }\] Ce n’est pratique, de plus en mulitpliant les t-test on multiplie egalement l’erreur toujours commiselors d’un test statistique. Chaque t-test est réalisé avec un risque \(\alpha\) (souvent pris à 5 %). Avec 15 tests indépendants la probabilité de faire au moins une erreur de type I augmente fortement. Le risque global devient largement supérieur à 5 %.

On tente alors de réaliser une ANOVA.

5. Conditions d’application de l’ANOVA
  1. Rappelez les conditions nécessaires à l’ANOVA à un facteur.
  2. En vous appuyant sur les histogrammes et le tableau des moyennes et écarts types, indiquez si elles sont raisonnablement satisfaites.
  3. Rappelez l’hypothèse nulle pour l’ANOVA

L’ANOVA repose sur un certain nombre d’hypothèses, dont la validité est nécessaire pour que le test statistique soit fiable :

  • Indépendance des observations. Chaque observation (ici chaque œuf de coucou) doit être indépendante des autres. Si deux œufs dans le même nid sont dépendants, les résultats pourraient être biaisés. En pratique s’assurer que les mesures proviennent de différents nids ou individus.

  • Normalité des résidus. Les résidus du modèle (différence entre chaque observation et la moyenne du groupe) doivent suivre une loi normale.

  • Homogénéité des variances. Les variances des groupes doivent être approximativement égales.

  • Indépendance. Chaque observation représente la longueur d’un œuf de coucou dans un nid donné. Les données semblent provenir de différents nids et espèces, donc on peut raisonnablement supposer l’indépendance.

  • Normalité des résidus. Les histogrammes par espèce montrent des distributions unimodales et symétriques, sans valeurs aberrantes extrêmes. La normalité exacte sera testée plus tard par Shapiro-Wilk, mais visuellement, les conditions de normalité semblent raisonnablement respectées.

  • Homogénéité des variances. Les écarts-types par groupe varient entre 0,685 et 1,07 mm. Les variances (écart-type au carré) sont donc proches les unes des autres. Comme déjà vu le rapport entre la plus grande et la plus petite variance est d’environ 1,55 (inférieur à 2), ce qui est généralement acceptable. Les histogrammes montrent des étalements similaires pour tous les groupes. Visuellement la condition d’homogénéité des variances semble respectée.

L’hypothèse nulle pour l’ANOVA est :

Toutes les espèces hôtes recoivent des oeufs de coucou de même longueur en moyenne.

Sur conseil d’un collaborateur on réalise un leveneTest.

leveneTest(egg_length ~ host_species, data = cuckooeggs)
Warning in leveneTest.default(y = y, group = group, ...): group coerced to
factor.
Levene's Test for Homogeneity of Variance (center = median)
       Df F value Pr(>F)
group   5  0.6397 0.6698
      114
6. Levene test
  1. Donner l’hypothèse nulle pour ce test.
  2. Interpréter ce test, que pouvez vous en conclure ?

Le Levene Test est un test paramétrique destiné à vérifier l’égalité des variances entre plusieurs groupes. L’hypothèse nulle pour ce test est :

Toutes les variances des groupes sont égales.

Ou encore les variances de longueurs d’oeufs sont égales. Le test donne p = 0,6698. Comme la p-value est largement supérieure à 0,05, nous acceptons l’hypyhèse nulle \(H_0\). Les variances sont donc considérées comme homogènes.

Ce collaborateur nous recommande vivement d’effectuer un shapiro.test. Nous en réalisons donc plusieurs.

by(cuckooeggs$egg_length, cuckooeggs$host_species, shapiro.test)
cuckooeggs$host_species: Hedge Sparrow

    Shapiro-Wilk normality test

data:  dd[x, ]
W = 0.94843, p-value = 0.5366

------------------------------------------------------------ 
cuckooeggs$host_species: Meadow Pipit

    Shapiro-Wilk normality test

data:  dd[x, ]
W = 0.93006, p-value = 0.009424

------------------------------------------------------------ 
cuckooeggs$host_species: Pied Wagtail

    Shapiro-Wilk normality test

data:  dd[x, ]
W = 0.96471, p-value = 0.7736

------------------------------------------------------------ 
cuckooeggs$host_species: Robin

    Shapiro-Wilk normality test

data:  dd[x, ]
W = 0.95212, p-value = 0.5239

------------------------------------------------------------ 
cuckooeggs$host_species: Tree Pipit

    Shapiro-Wilk normality test

data:  dd[x, ]
W = 0.89772, p-value = 0.08786

------------------------------------------------------------ 
cuckooeggs$host_species: Wren

    Shapiro-Wilk normality test

data:  dd[x, ]
W = 0.93295, p-value = 0.3019
anova_res <- aov(egg_length ~ host_species, data = cuckooeggs)
shapiro.test(residuals(anova_res))

    Shapiro-Wilk normality test

data:  residuals(anova_res)
W = 0.9804, p-value = 0.07761
7. Shapiro test
  1. Donnez l’hypothèse nulle pour le shapiro.test.
  2. Interprétez chacun de ces shapiro.test.
  3. Etaient ils tous nécessaire ?
  4. Que pouvez vous en conclure pour l’ANOVA ?

L’hypothèse nulle du Shapiro-Wilk test est :

Les données suivent une distribution normale.

En pratique :

  • si la p-value > 0,05, on considère que l’hypothèse nulle est accepté et que la normalité donc est acceptée

  • si la p-value < 0,05, on considère que l’hypothèse nulle est rejeté et que la normalité est rejetée

Espèce p-value Interprétation
Hedge Sparrow 0,537 p > 0,05 → \(H_0\) acceptée → normalité acceptée
Meadow Pipit 0,009 p < 0,05 → \(H_0\) rejetée → normalité rejetée
Pied Wagtail 0,774 p > 0,05 → \(H_0\) acceptée → normalité acceptée
Robin 0,524 p > 0,05 → \(H_0\) acceptée → normalité acceptée
Tree Pipit 0,088 p > 0,05 → \(H_0\) acceptée → normalité acceptée
Wren 0,302 p > 0,05 → \(H_0\) acceptée → normalité acceptée

Meadow Pipit présente une p-value < 0,05, donc la distribution sera considérée comme non normale. Les autres espèces n’indiquent aucune violation significative de normalité.

Shapiro-Wilk sur les résidus de l’ANOVA

shapiro.test(residuals(anova_res))

    Shapiro-Wilk normality test

data:  residuals(anova_res)
W = 0.9804, p-value = 0.07761

On obtient p-value = 0,078 > 0.05. L’hypothèse nulle est acceptée, donc la normalité est acceptée.

L’ANOVA repose sur la normalité des résidus, pas nécessairement des groupes pris séparément. Un groupe peut être légèrement non normal (ex : Meadow Pipit), mais si les résidus globaux sont normaux, l’ANOVA reste valide. Tester chaque groupe séparément est utile pour l’inspection exploratoire, mais ce n’est pas la condition clé pour l’ANOVA.

Si les résidus ne sont pas normaux, les p-values de l’ANOVA peuvent être inexactes, le risque d’erreur de type I (faux positif) peut augmenter. Cependant, l’ANOVA est robuste aux violations légères, surtout avec des échantillons de taille raisonnable (ici entre 15 et50 individus par groupe).

D’apres la question 6 on a montré l’homogénité des variances, et on vient de vérifié la normalité des risidus. L’ANOVA peut donc être appliquée de manière fiable.

Une fois nos shapiro.test réalisés, un autre collaborateur examine notre travail et nous indique qu’il aurait été pertinent de produire un qqplot. Nous tentons alors de tracer ce graphique.

qqnorm(residuals(anova_res))
qqline(residuals(anova_res))

8. Q-Q plot
  1. Rappelez la définition d’un q-q plot et expliquez en quoi l’observation de ce collaborateur était pertinente.
  2. Analysez et interprétez ce graphique.
  3. Ces résultats concordent-ils avec le test de Shapiro précédemment effectué ?

Un Q-Q plot est un graphique permettant de comparer les quantiles observés des données (des résidus ici) et les quantiles théoriques d’une loi normale.

  • Sur l’axe X : quantiles théoriques d’une loi normale

  • Sur l’axe Y : quantiles observés des résidus

  • Si les points se rapprochent d’une droite diagonale, cela indique que les données suivent approximativement une loi normale

  • Les écarts significatifs par rapport à la droite indiquent des déviations à la normalité (asymétrie, queues longues, outliers)

  • Il permet de compléter le Shapiro-Wilk test par une inspection visuelle

  • Le Q-Q plot est particulièrement utile car il permet de détecter des déviations légères ou des outliers que les tests statistiques seuls pourraient ne pas révéler

  • Les tests de normalité (Shapiro-Wilk) sont sensibles au nombre d’observations, pour de grands échantillons des écarts mineurs peuvent rendre le test significatif, pour de petits échantillons des écarts importants peuvent ne pas être détectés. Le Q-Q plot fournit une inspection visuelle complémentaire.

Ici les points suivent assez bien la droite diagonale. Quelques écarts peuvent apparaître aux extrémités, ce qui est courant dans les données biologiques. Les écarts légers aux extrémités correspondent aux queues de distribution (valeurs extrêmes légèrement plus petites ou plus grandes que prévu). Aucune déviation majeure n’est visible.

Le Shapiro-Wilk test sur les résidus avait permis d’accepté l’hypothése de nomalité. Le Q-Q plot confirme visuellement cette conclusion.

summary(anova_res)
              Df Sum Sq Mean Sq F value   Pr(>F)    
host_species   5  42.94   8.588   10.39 3.15e-08 ***
Residuals    114  94.25   0.827                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
9. Résultat de l’ANOVA
  1. D’après les résultats de l’ANOVA, peut-on conclure que l’effet de l’espèce hôte sur la taille des œufs est statistiquement significatif ?
  2. L’ANOVA permet-elle de déterminer exactement quelles espèces présentent des effets différents ?

On obtient une p-value égale à \(3,15 \times 10^{-8}\). Cette valeur est extrêmement inférieure aux seuils usuels de 0,05. On rejette très fortement l’hypothèse nulle. Oui, l’effet de l’espèce hôte sur la taille des œufs de coucou est hautement statistiquement significatif. Autrement dit il est extrêmement improbable que les différences observées de longueur d’œufs soient dues uniquement au hasard. L’espèce hôte explique une partie significative de la variabilité observée.

L’ANOVA met en évidence un effet global significatif de l’espèce hôte sur la longueur des œufs de coucou. Cependant, elle ne permet pas d’identifier quelles espèces diffèrent entre elles. Un test post-hoc est donc nécessaire pour comparer les moyennes deux à deux.

Toujours le même collaborateur nous parle déffecteuer un test post hoc. On le réalise sans trop savoir ce que l’on est en train de tester.

tukey <- TukeyHSD(anova_res)
tukey
  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = egg_length ~ host_species, data = cuckooeggs)

$host_species
                                  diff          lwr         upr     p adj
Meadow Pipit-Hedge Sparrow -0.82253968 -1.629133605 -0.01594576 0.0428621
Pied Wagtail-Hedge Sparrow -0.21809524 -1.197559436  0.76136896 0.9872190
Robin-Hedge Sparrow        -0.54642857 -1.511003196  0.41814605 0.5726153
Tree Pipit-Hedge Sparrow   -0.03142857 -1.010892769  0.94803563 0.9999990
Wren-Hedge Sparrow         -1.99142857 -2.970892769 -1.01196437 0.0000006
Pied Wagtail-Meadow Pipit   0.60444444 -0.181375330  1.39026422 0.2324603
Robin-Meadow Pipit          0.27611111 -0.491069969  1.04329219 0.9021876
Tree Pipit-Meadow Pipit     0.79111111  0.005291337  1.57693089 0.0474619
Wren-Meadow Pipit          -1.16888889 -1.954708663 -0.38306911 0.0004861
Robin-Pied Wagtail         -0.32833333 -1.275604766  0.61893810 0.9155004
Tree Pipit-Pied Wagtail     0.18666667 -0.775762072  1.14909541 0.9932186
Wren-Pied Wagtail          -1.77333333 -2.735762072 -0.81090459 0.0000070
Tree Pipit-Robin            0.51500000 -0.432271433  1.46227143 0.6159630
Wren-Robin                 -1.44500000 -2.392271433 -0.49772857 0.0003183
Wren-Tree Pipit            -1.96000000 -2.922428738 -0.99757126 0.0000006
10. Test post-hoc - Tukey test
  1. Rappelez l’objectif d’un test post-hoc après une ANOVA.
  2. D’après les résultats du test de Tukey, quelles paires d’espèces présentent des différences significatives ?
  3. Quelles conclusions peut-on tirer de ces résultats ?

Après avoir mis en évidence, grâce à l’ANOVA, un effet global significatif de l’espèce hôte sur la longueur des œufs de coucou, il est nécessaire d’aller plus loin dans l’analyse afin de comprendre quelles espèces diffèrent réellement entre elles.

C’est précisément le rôle d’un test post-hoc, ici le test de Tukey.

Un test post-hoc permet de comparer toutes les paires de groupes deux à deux, tout en contrôlant le risque global d’erreur de type I (fausse détection de différences). Sans correction post-hoc, multiplier les comparaisons augmenterait artificiellement le risque de conclure à tort.

Le test de Tukey est particulièrement adapté lorsque toutes les comparaisons par paires sont d’intérêt, les tailles d’échantillons sont comparables, et les variances sont homogènes (condition vérifiée par le test de Levene).

Les paires pour lesquelles la différence est statistiquement significative :

Comparaison Différence de moyennes (mm) IC 95 % p-value ajustée Interprétation
Meadow Pipit – Hedge Sparrow −0,82 [−1,63 ; −0,02] 0,043 Hedge Sparrow > Meadow Pipit
Tree Pipit – Meadow Pipit +0,79 [0,01 ; 1,58] 0,047 Tree Pipit > Meadow Pipit
Wren – Hedge Sparrow −1,99 [−2,97 ; −1,01] < 10⁻⁶ Wren ≪ Hedge Sparrow
Wren – Meadow Pipit −1,17 [−1,95 ; −0,38] 4,9 × 10⁻⁴ Wren ≪ Meadow Pipit
Wren – Pied Wagtail −1,77 [−2,74 ; −0,81] 7 × 10⁻⁶ Wren ≪ Pied Wagtail
Wren – Robin −1,45 [−2,39 ; −0,50] 3,2 × 10⁻⁴ Wren ≪ Robin
Wren – Tree Pipit −1,96 [−2,92 ; −1,00] < 10⁻⁶ Wren ≪ Tree Pipit

Toutes les comparaisons impliquant Wren sont significatives.

Ci-dessous les paires pour lesquelles la comparaison est non significative.

Comparaison p-value ajustée Conclusion
Hedge Sparrow – Tree Pipit 1,00 Pas de différence
Hedge Sparrow – Pied Wagtail 0,99 Pas de différence
Hedge Sparrow – Robin 0,57 Pas de différence
Meadow Pipit – Pied Wagtail 0,23 Pas de différence
Meadow Pipit – Robin 0,90 Pas de différence
Pied Wagtail – Robin 0,92 Pas de différence
Pied Wagtail – Tree Pipit 0,99 Pas de différence
Robin – Tree Pipit 0,62 Pas de différence

Ce tableau résume les résultats sous forme de groupes homogènes.

Groupe Espèces Interprétation
Groupe A (œufs les plus grands) Hedge Sparrow, Tree Pipit, Pied Wagtail, Robin Moyennes élevées, pas de différences significatives entre elles
Groupe B (intermédiaire) Meadow Pipit Moyenne légèrement plus faible
Groupe C (œufs les plus petits) Wren Moyenne significativement plus faible que toutes les autres

Le test post-hoc de Tukey permet de comparer les moyennes deux à deux tout en contrôlant le risque d’erreur lié aux comparaisons multiples. Les résultats montrent que l’espèce Wren se distingue significativement de toutes les autres, avec des œufs de coucou significativement plus petits. D’autres différences plus modestes sont observées entre Meadow Pipit et certaines espèces. En revanche, plusieurs espèces présentent des moyennes statistiquement similaires. Ces résultats indiquent que la taille des œufs de coucou dépend finement de l’espèce hôte, ce qui suggère une adaptation évolutive.

Exercice 2

Le jeu de données utilisé dans cet examen est inspiré d’une étude publiée dans la revue Cell, Petropoulos et al. (2016), où des chercheurs ont mesuré l’activité de nombreux gènes dans des cellules provenant d’embryons humains très précoces. Leur objectif était d’observer comment les cellules évoluent au cours du développement et comment elles se différencient en plusieurs types cellulaires.

Pour notre exercice, nous utilisons une version simplifiée de ce type de données. Le fichier contient :

  • 300 gènes (chaque ligne correspond à un gène différent)

  • 12 échantillons (chaque colonne correspond à une condition biologique), représentant différents jours de développement et différents types de cellules :

    • Exemples : Day_5_EPI, Day_5_TE, Day_6_PE, etc.

  • Les variables du fichier sont donc :

    • Gene : nom du gène

    • 12 variables quantitatives (une par condition), correspondant à l’expression du gène dans chaque échantillon (mesure numérique)

L’objectif de l’Analyse en composantes principales est d’identifier les grands axes qui résument les principales différences d’expression entre ces 12 conditions, et de visualiser si certaines conditions se regroupent selon des profils similaires.

Le fichier de données est mmc3.xlsx.

data  = read_excel("data_raw/mmc3.xlsx")
head(data)
# A tibble: 6 × 13
  Gene    Day_3 Day_4 Pre_Day_5 Day_5_EPI Day_5_PE Day_5_TE Day_6_EPI Day_6__PE
  <chr>   <dbl> <dbl>     <dbl>     <dbl>    <dbl>    <dbl>     <dbl>     <dbl>
1 SEPT6     1.5   0         0.2       2.2      0.6      0.3       9.8       0.7
2 AARS2     2.3  13.8      17.3      44.1     19.5      8.5      21.8       7.5
3 ABCG2     0.2   0.3       7.6       3.3     10.4     35.1      23        54  
4 ABHD12B   5.8  11        16.7      33.3     17       12.3      57.4      18.3
5 ABHD6     0.8   4.2       9.7       7.5     29.2      8.1      11.8      14.8
6 ACE       0.3  17.5      10.3      15.4      6.7      3.9      11.1       1.3
# ℹ 4 more variables: Day_6_TE <dbl>, Day_7_EPI <dbl>, Day_7_PE <dbl>,
#   Day_7_TE <dbl>
var.quanti = sapply(data, is.numeric)
data.quanti = data[, var.quanti]
head(data.quanti)
# A tibble: 6 × 12
  Day_3 Day_4 Pre_Day_5 Day_5_EPI Day_5_PE Day_5_TE Day_6_EPI Day_6__PE Day_6_TE
  <dbl> <dbl>     <dbl>     <dbl>    <dbl>    <dbl>     <dbl>     <dbl>    <dbl>
1   1.5   0         0.2       2.2      0.6      0.3       9.8       0.7      0.4
2   2.3  13.8      17.3      44.1     19.5      8.5      21.8       7.5      4.8
3   0.2   0.3       7.6       3.3     10.4     35.1      23        54       71.3
4   5.8  11        16.7      33.3     17       12.3      57.4      18.3      9.8
5   0.8   4.2       9.7       7.5     29.2      8.1      11.8      14.8      8.8
6   0.3  17.5      10.3      15.4      6.7      3.9      11.1       1.3      0.8
# ℹ 3 more variables: Day_7_EPI <dbl>, Day_7_PE <dbl>, Day_7_TE <dbl>
1. Question théorique
  1. Combien de gènes et de conditions contient le jeu de données ?
  2. Quelles sont les variables quantitatives ?
  3. Pourquoi est-il important de distinguer les variables quantitatives et qualitatives avant l’analyse ?
  4. Expliquez en quelques phrases l’objectif de l’ACP. Pourquoi cette méthode est-elle utilisée ?

Le jeu de données est structuré sous forme de tableau où :

  • Chaque ligne correspond à un gène

  • Chaque colonne correspond à une variable

À partir de la description et de l’aperçu avec head(data), on observe :

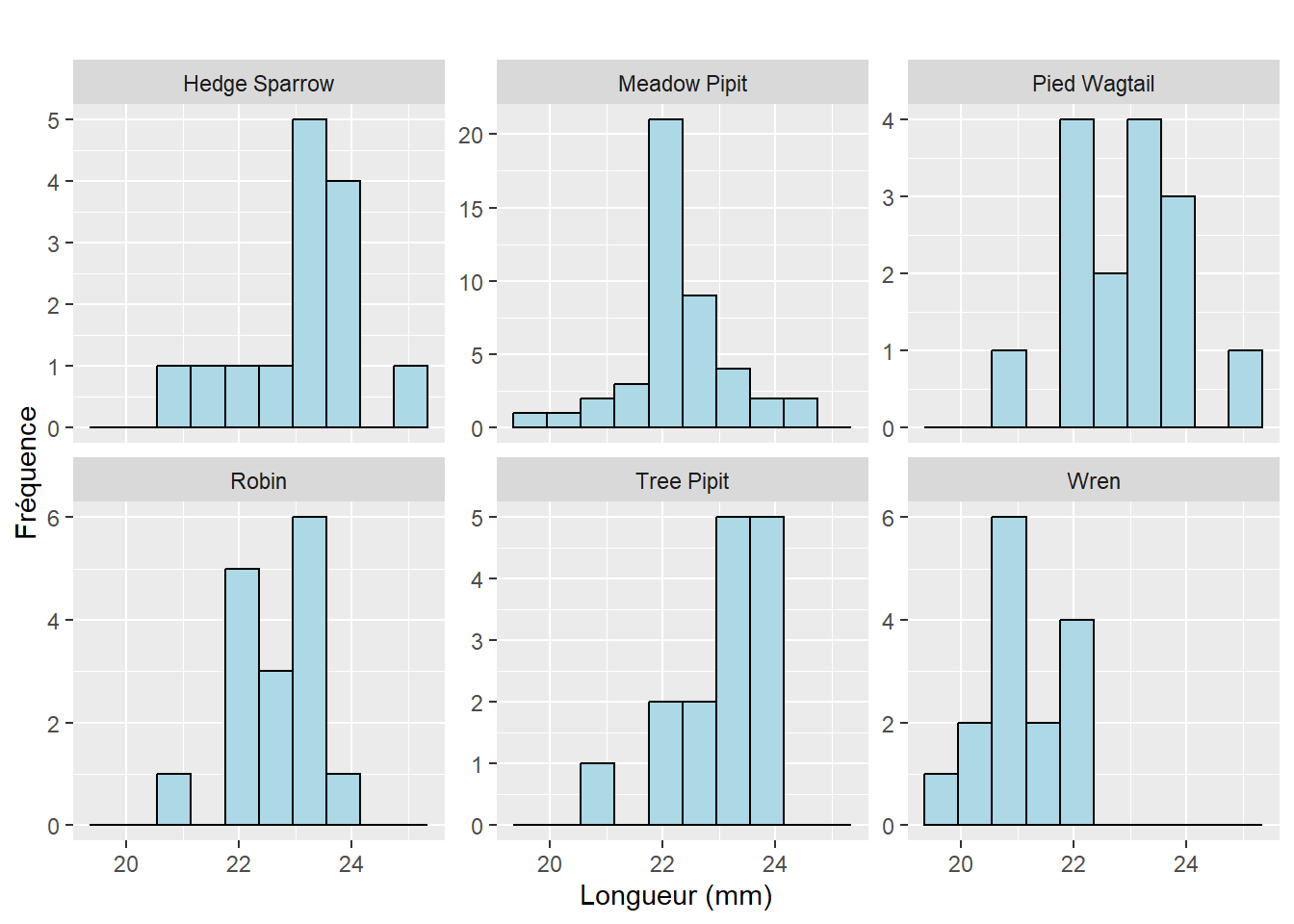
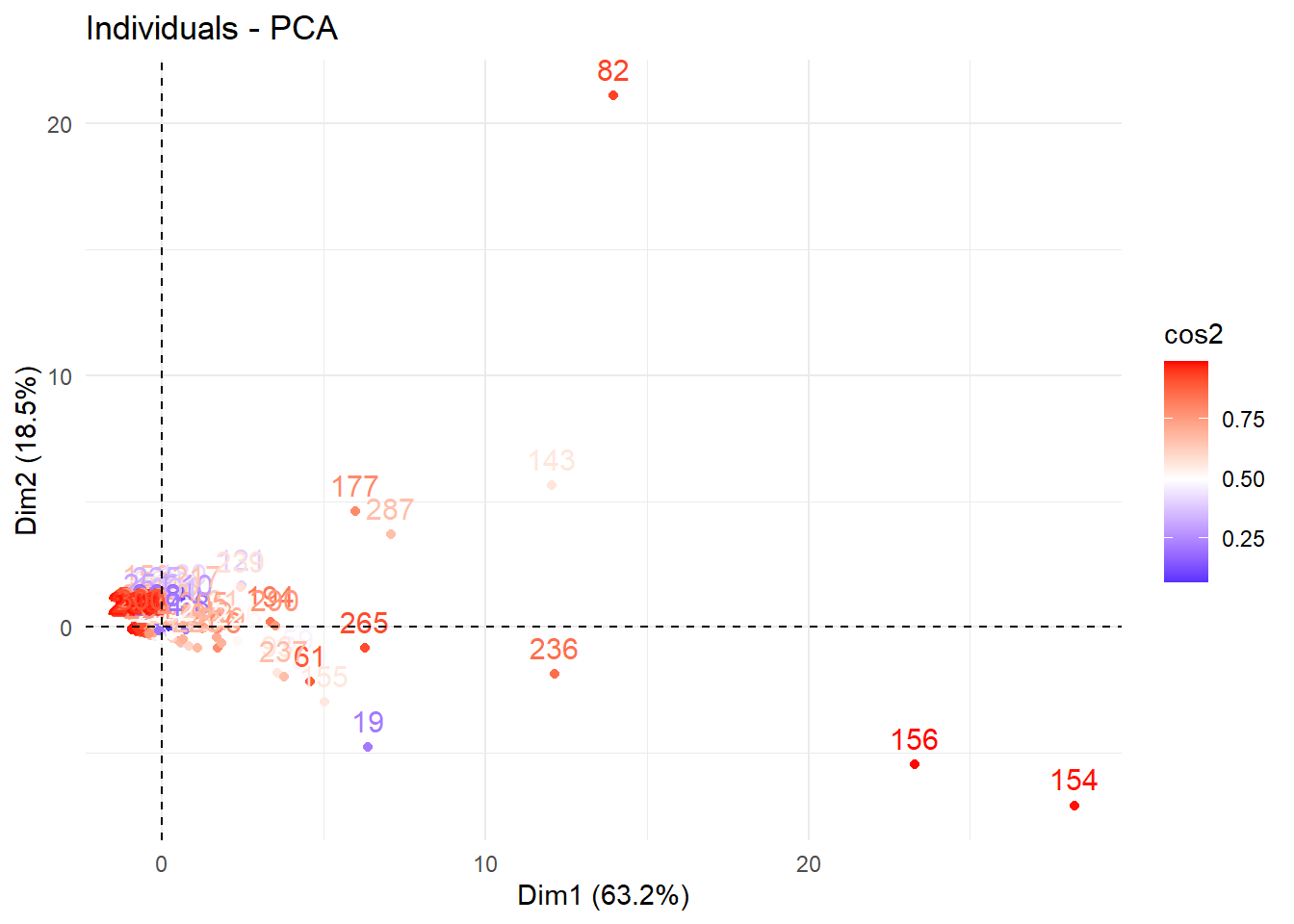
  • 300 lignes, ce qui signifie que 300 gènes distincts sont analysés

  • 13 colonnes au total, parmi lesquelles :

    • 1 colonne qualitative : Gene (nom du gène)

    • 12 colonnes quantitatives correspondant aux conditions biologiques. Ces 12 conditions représentent :

      • Différents jours de développement embryonnaire (Day 3 à Day 7)
      • Différents types cellulaires :
        • EPI (Epiblaste)
        • PE (Primitive Endoderm)
        • TE (Trophectoderme)

Le jeu de données contient donc 300 gènes (individus statistiques) décrits par 12 conditions biologiques (variables quantitatives).

Les variables quantitatives sont celles qui sont de type numérique, qui représentent des mesures continues, et peuvent être comparées par des opérations mathématiques (moyenne, variance, corrélation). Dans ce jeu de données, il s’agit des 12 colonnes évoquées plus haut :

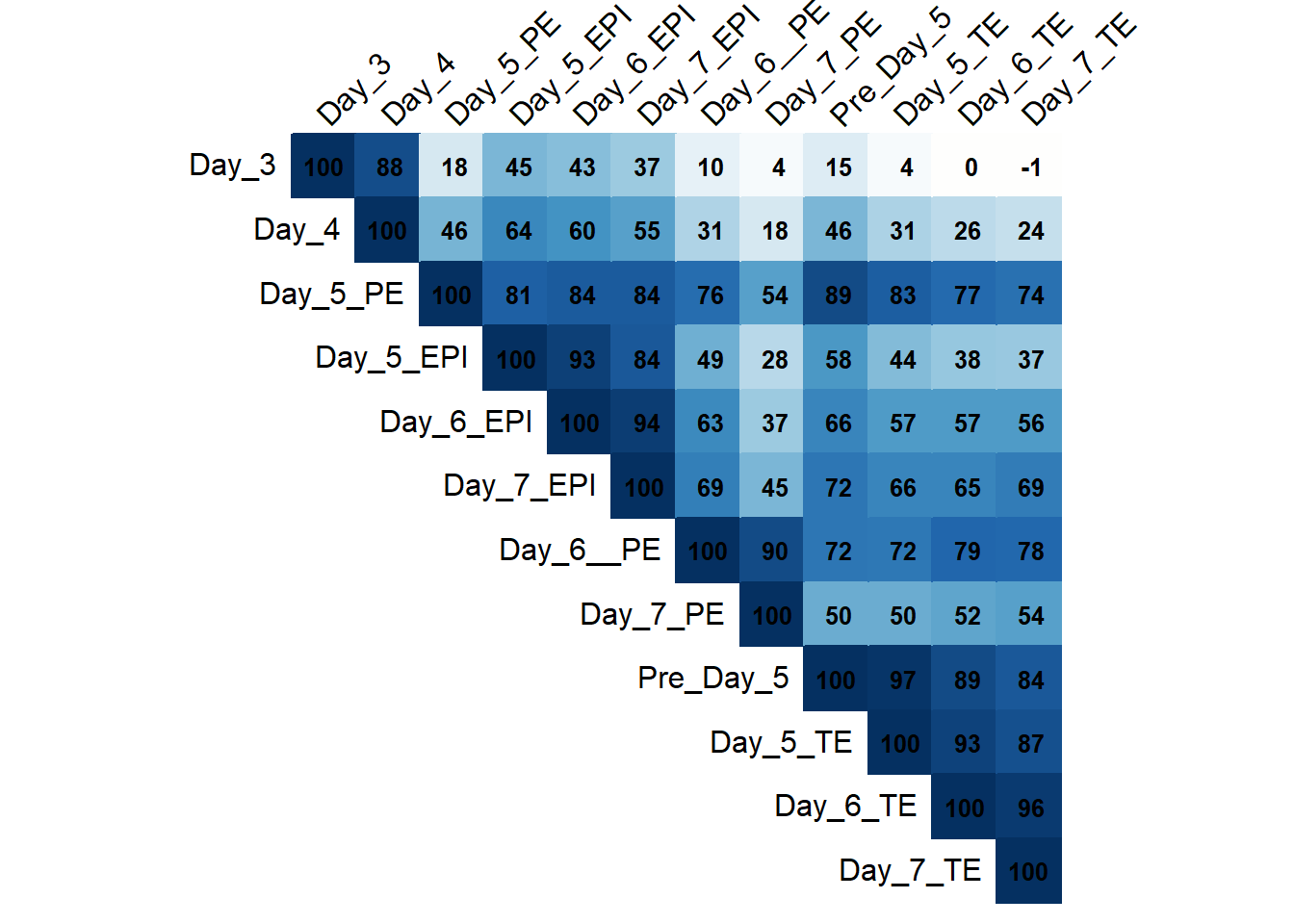
Day_3, Day_4, Pre_Day_5, Day_5_EPI, Day_5_PE, Day_5_TE, Day_6_EPI, Day_6_PE, Day_6_TE, Day_7_EPI, Day_7_PE et Day_7_TE.

Chaque valeur numérique correspond à un niveau d’expression génique mesuré pour un gène donné dans une condition biologique précise.

L’Analyse en Composantes Principales est une méthode algébrique. Elle repose sur :

  • Le calcul de variances

  • Le calcul de covariances ou de corrélations

  • La diagonalisation d’une matrice numérique

Ces concepts mathématiques n’ont de sens que pour des variables quantitatives. Conséquences si cette distinction n’est pas faite, inclure une variable qualitative dans une ACP entraînerait une impossibilité mathématique ! Cette sélection garantit la validité statistique de l’analyse.

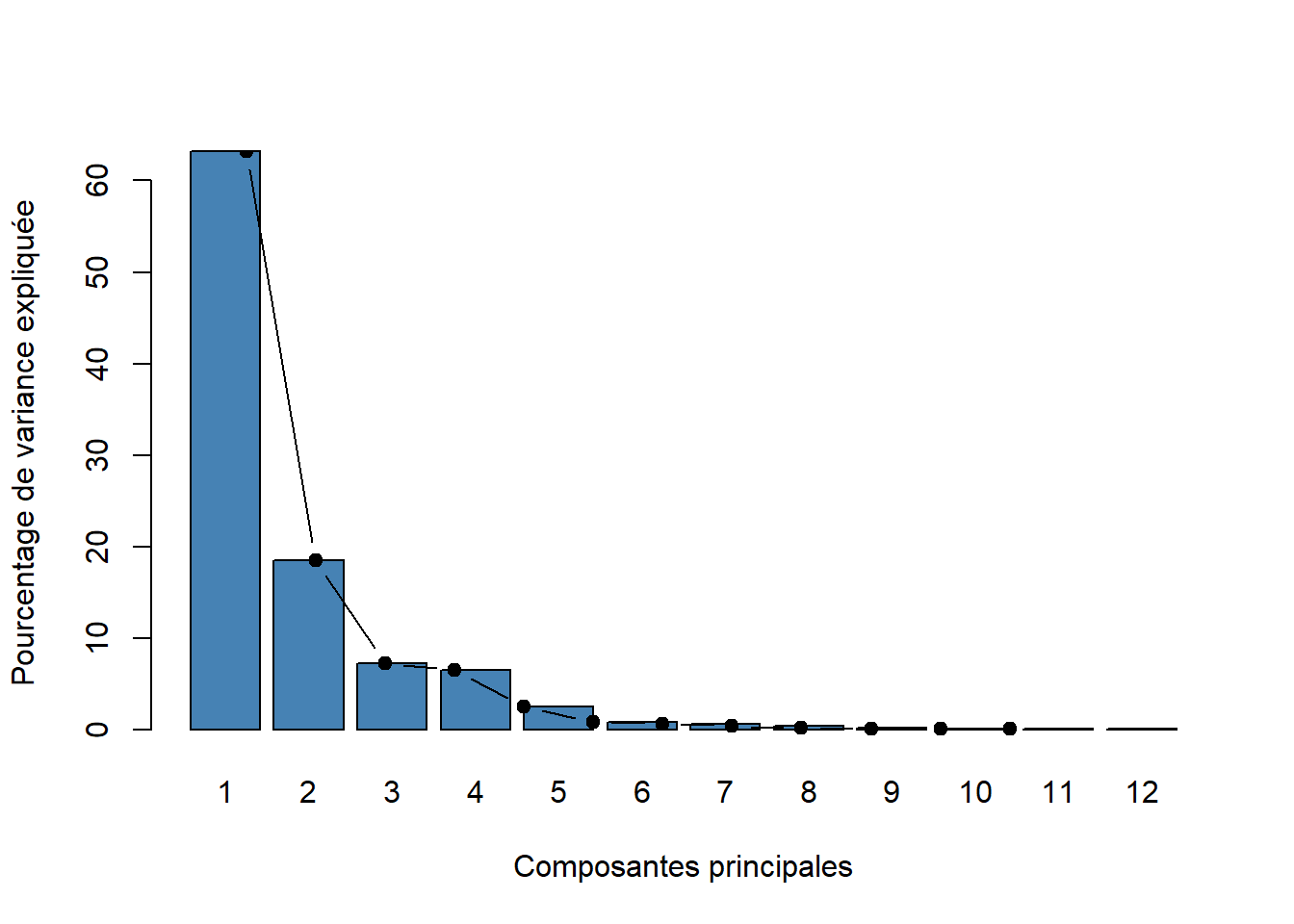
L’Analyse en Composantes Principales vise à résumer l’information contenue dans un grand nombre de variables corrélées par un petit nombre de variables non corrélées, appelées composantes principales. Plus précisément, cette analyse permet de :

  • Réduire la dimension des données

  • Conserver un maximum de variance

  • Identifier les structures dominantes

  • Faciliter la visualisation et l’interprétation de corrlations entre variables

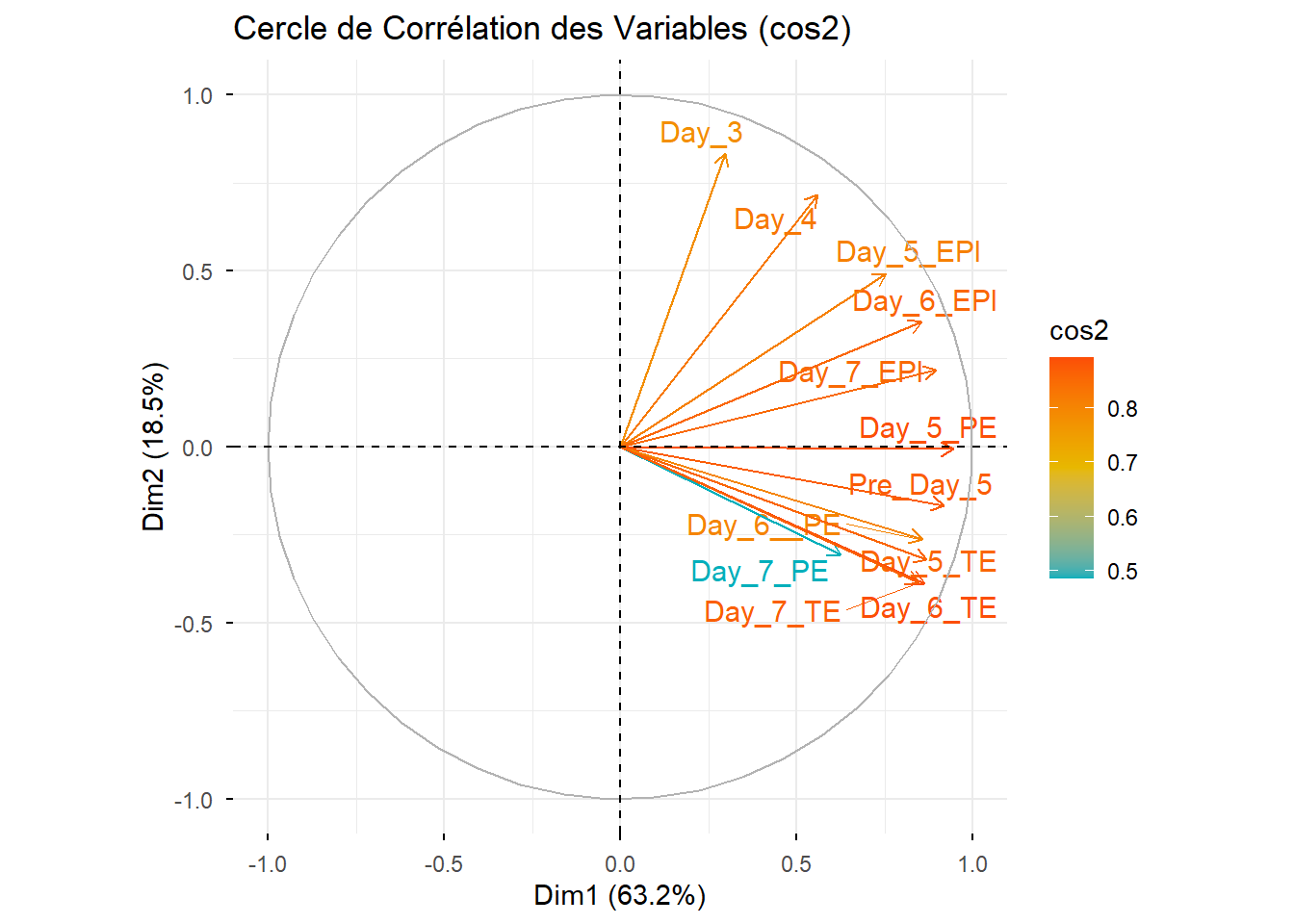
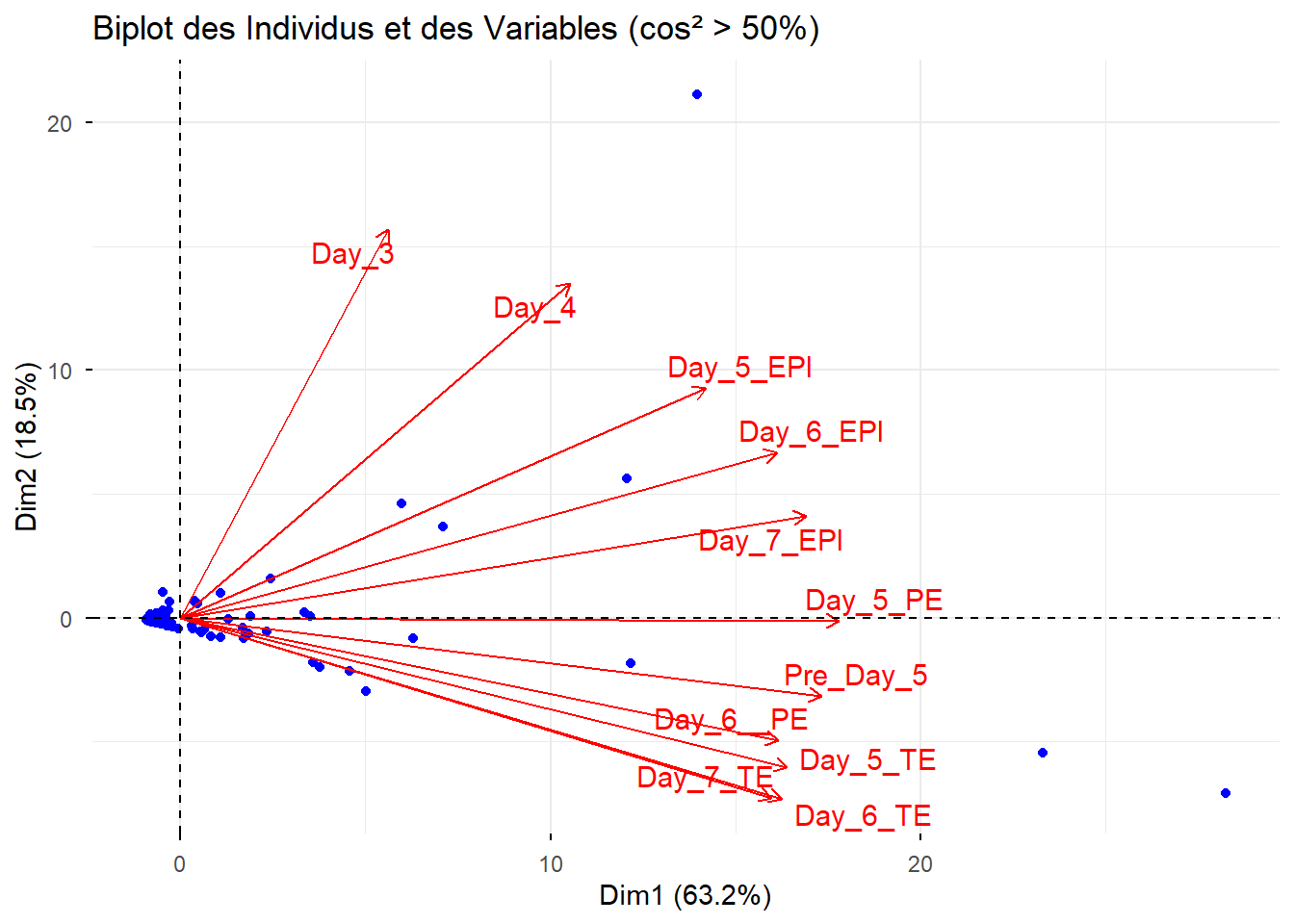
Cette analyse est particulièrement adaptée ici car il y a un grand nombre de variables, les 12 conditions biologiques fortement dépendantes biologiquement (mêmes processus de développement). On s’attend donc à de fortes corrélations, ce qui est une situation idéale pour l’ACP. L’étude ne cherche pas à tester une hypothèse précise, mais à :

  • Explorer les données

  • Détecter des tendances

  • Mettre en évidence des regroupements

L’ACP est une méthode exploratoire non supervisée, parfaitement adaptée à cet objectif. Dans ce contexte, l’ACP doit permettre de :

  • Identifier si les conditions se regroupent :
    • Par jour de développement
    • Par type cellulaire
  • Comprendre quels ensembles de conditions :
    • Partagent des profils d’expression similaires
    • S’opposent sur certains axes
Matrice.Correlation <- cor(data.quanti, use = "complete.obs")

corrplot(Matrice.Correlation, 
         method = "color", 
         type = "upper", 
         order = "hclust",
         tl.col = "black", 
         tl.srt = 45, 
         addCoef.col = "black",
         cl.pos = "n",
         cl.cex = 1.2,
         addCoefasPercent = TRUE,
         number.cex = 0.8)

data.quanti = data[, var.quanti]
2. Matrice de corrélation
  1. Quelles conditions semblent fortement corrélées ? Quelles conditions semblent peu corrélées ?
  2. Que peut-on déduire de ces corrélations pour l’analyse en composantes principales ?

Les conditions qui montrent des valeurs proches de 100 dans la matrice sont fortement corrélées.

Conditions fortement corrélées Interprétation
Day_6_EPI et Day_7_EPI Même type cellulaire (EPI) à des jours consécutifs
Day_5_TE et Day_6_TE Même type cellulaire (EPI) à des jours consécutifs
Day_5_PE et Day_6_PE Même type cellulaire (EPI) à des jours consécutifs

  • Ces cellules continuent leur programme de développement spécifique.

  • Les gènes exprimés dans un type cellulaire donné restent actifs à des niveaux comparables au cours des jours successifs.

Les conditions qui montrent des valeurs proches de 0 dans la matrice sont faiblement corrélées.

Conditions faiblement corrélées Interprétation
Day_3 et Day_7_TE Gènes exprimés très différemment ; changement de programme de développement
Day_3 et Day_5_PE Profils biologiques distincts.
EPI vs TE ou PE Très différents

Les variables fortement corrélées apportent la même information (exemple : Day_6_EPI et Day_7_EPI). Pour une ACP, cette redondance est utile. L’ACP combine les variables corrélées pour créer un axe principal. Cela permet de résumer l’information avec moins de composantes.

  • L’axe 1 de l’ACP capturera probablement la variation commune à ces jours consécutifs pour un type cellulaire.

  • Les variables faiblement corrélées ou négativement corrélées introduisent des axes supplémentaires.

Observation Implication pour l’ACP
Corrélation forte entre conditions similaires Ces variables seront résumées par le même axe principal
Corrélation faible entre types cellulaires ou jours éloignés Ces différences seront capturées par des axes secondaires
Bloc de corrélations Permet d’identifier des groupes biologiques cohérents avant l’ACP 
data.CR <- scale(data.quanti,center = TRUE,scale=TRUE)
pca.data <- PCA(data.CR, graph = FALSE)
vp = pca.data$eig
vp
         eigenvalue percentage of variance cumulative percentage of variance
comp 1  7.585892122            63.21576768                          63.21577
comp 2  2.217238058            18.47698382                          81.69275
comp 3  0.873147907             7.27623255                          88.96898
comp 4  0.776224795             6.46853996                          95.43752
comp 5  0.293172253             2.44310211                          97.88063
comp 6  0.097438066             0.81198388                          98.69261
comp 7  0.072100242             0.60083535                          99.29345
comp 8  0.046325556             0.38604630                          99.67949
comp 9  0.016444017             0.13703347                          99.81653
comp 10 0.013633402             0.11361169                          99.93014
comp 11 0.005016309             0.04180257                          99.97194
comp 12 0.003367273             0.02806061                         100.00000
barplot(vp[, 2], 
        names.arg=1:nrow(vp), 
        main = "",
        xlab = "Composantes principales",
        ylab = "Pourcentage de variance expliquée",
        col ="steelblue")

lines(x = 1:nrow(vp), 
      vp[, 2], 
      type="b", 
      pch=19, 
      col = "black")

3. Variance expliquée
  1. Que représente la variance expliquée par chaque composante principale ?
  2. Combien de composantes principales retiendriez-vous pour représenter l’essentiel de l’information ? Justifiez votre réponse.
  3. Quelle proportion de variance est expliquée par les deux premières composantes ?

Dans une ACP, chaque composante principale est une combinaison linéaire des variables originales.

  • La première composante principale (Dim 1) est construite pour maximiser la variance totale des données projetées sur cette dimension.

  • La deuxième composante principale (Dim 2) maximise la variance restante sous contrainte d’orthogonalité à la première composante principale.

  • Et ainsi de suite pour les axes suivants.

La variance expliquée par une composante principale correspond à :

\[\text{Variance expliquée de Dim i} = \frac{\text{valeur propre (eigenvalue) de Dim i}}{\text{somme des valeurs propres}} \times 100\]

La valeur propre (eigenvalue) mesure la quantité de variance capturée par l’axe. Plus la valeur propre est grande, plus l’axe est informative.

Ici chaque axe représente un profil d’expression génétique combiné :

  • Dim 1 : direction qui distingue les conditions les plus différentes

  • Dim 2 : direction qui capture le deuxième contraste le plus important

La variance expliquée indique combien de l’information totale (différences d’expression entre conditions) est conservée sur cet axe. Exemple : si Dim 1 explique 63 %, cela signifie que 63 % de la variabilité totale entre conditions est résumée sur ce seul axe.

Composante Eigenvalue % Variance % Cumulée
Dim 1 7.586 63.2 % 63.2 %
Dim 2 2.217 18.5 % 81.7 %
Dim 3 0.873 7.3 % 88.97 %
Dim 4 0.776 6.47 % 95.44 %
Dim 5 0.293 2.44 % 97.88 %

  • Dim 1 (63 %) : capture la majeure partie de la variation, probablement liée aux différences temporelles globales et aux types cellulaires majeurs

  • Dim 2 (18.5 %) : capture les différences secondaires,

  • Axes suivants (<10 %) : capturent des variations mineures, bruit ou différences très spécifiques

Seules les composantes avec une valeur propre > 1 sont considérées comme significatives. Ici :

  • Dim 1 : 7.586 → OK
  • Dim 2 : 2.217 → OK
  • Dim 3 : 0.873 < 1 → moins informative

On peut utiliser le critère du coude (scree plot). Il suffit d’observer le point où la courbe se stabilise (diminution rapide → “coudé”). Ici le coude est évident après Dim 2, les axes suivants apportent peu de variance.

On peut également utiliser un critère de variance cumulée, c’est à dire retenir des axes qui expliquent 80 % ou plus de la variance. Ici les 2 premiers axes expliquent 63.2 + 18.5 ≈ 81.7 %. Cela est suffisant pour résumer l’information principale dans 2 axes.

La proportion de variance expliquée par les deux premières composantes principales est 63.2 + 18.5 = 81.7 %. Plus de 80 % de l’information totale est conservée dans un plan 2D. Cela justifie la visualisation des individus et des variables sur un plan factoriel. Les axes 1 et 2 suffisent pour mettre en évidence les structures principales des données (regroupements, oppositions, profils dominants)

Synthèse :

Question Réponse détaillée
Que représente la variance expliquée ? La proportion de la variation totale capturée par chaque axe. Plus elle est grande, plus l’axe est informatif.
Combien de composantes retenir ? 2 axes principaux. Justification : valeur propre >1, coude du scree plot, variance cumulée >80 %.
Variance cumulée Dim1+Dim2 81.7 % → suffisant pour une bonne représentation des données.
Utilité Résumer la majorité de l’information, visualiser les relations entre gènes et conditions, réduire le bruit. 
fviz_pca_var(pca.data, 
             col.var = "cos2",
             gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
             repel = TRUE,
             title = "Cercle de Corrélation des Variables (cos2)")

4. Cercle de corrélation
  1. Identifiez deux variables fortement corrélées et deux variables faiblement corrélées.
  2. Que signifie la longueur et l’orientation des flèches ?
  3. Quelles variables ont une contribution importante sur l’axe 2?

Le cercle de corrélation est un outil graphique qui permet de visualiser :

  • La relation entre variables quantitatives et les axes principaux

  • Les corrélations entre variables

  • La contribution de chaque variable à chaque axe

Deux variables sont fortement corrélées si leurs flèches sont proches et orientées suivant la même direction. L’angle entre elles est proche de 0°.

Exemples attendus dans ce jeu de données :

Variables fortement corrélées Justification
Day_6_EPI et Day_7_EPI Même type cellulaire, jours consécutifs → profils d’expression similaires
Day_5_TE et Day_6_TE Même type cellulaire TE → corrélation positive élevée

Deux variables sont faiblement corrélées si leurs flèches sont perpendiculaires (angle ≈ 90°).

Exemples attendus :

Variables faiblement corrélées Justification
Day_3 et Day_7_TE Jour très éloigné et type cellulaire différent → profils indépendants
Day_4 et Day_6_PE Flèches orthogonales → absence de corrélation linéaire

La longueur des flèches représente la qualité de représentation sur le plan factoriel.

  • Longue flèche → la variable est bien représentée, proche du plan choisi (Dim1 × Dim2)

  • Courte flèche → variable mal représentée, sa variance est surtout sur d’autres axes

Exemple pratique :

  • Day_6_EPI : longue flèche → forte contribution aux axes principaux

  • Day_7_PE : courte flèche → beaucoup de variance sur axes non représentés (Dim3, Dim4…)

L’orientation des flèches, vue par l’angle entre flèches traduit la corrélation entre variables :

  • Angle proche de 0° → corrélation positive forte

  • Angle proche de 180° → corrélation négative forte

  • Angle proche de 90° → variables indépendantes

Ici les flèches proches traduisent des types cellulaires avec profils similaires, et des flèches perpendiculaires traduisent des types cellulaires différents ou jours éloignés.

Sur le cercle de corrélation Day_3 et Day_4 ont des flèches longues et fortement orientées verticalement (Dim 2). Cela indique qu’elles contribuent de manière significative à l’axe 2.

head(pca.data$ind$coord)
       Dim.1       Dim.2       Dim.3         Dim.4       Dim.5
1 -0.8860388 -0.05653948 -0.05987579  0.0326202352  0.03833300
2 -0.6057873  0.10852636 -0.12243416 -0.0690008780 -0.10503767
3 -0.3699260 -0.31957924  0.03212768  0.1043982993  0.31567397
4 -0.5063049  0.11052344 -0.11409912 -0.1403434496  0.02666491
5 -0.6891486 -0.07722587 -0.02877404  0.0005839167 -0.07581851
6 -0.7792027  0.06145232 -0.06881027  0.0769645114 -0.05851516
fviz_pca_ind(pca.data,  col.ind="cos2") +
  scale_color_gradient2(low="blue", mid="white", high="red", midpoint=0.50) +
  theme_minimal()

# Filtrer les individus avec cos² > 50%
ind_cos2 <- apply(pca.data$ind$cos2, 1, max) > 0.5

# Filtrer les variables avec cos² > 50%
var_cos2 <- apply(pca.data$var$cos2, 1, max) > 0.5

# Créer un graphique combiné des individus et des variables
fviz_pca_biplot(pca.data,
                select.ind = list(cos2 = 0.5), # Sélectionner les individus avec cos² > 50%
                select.var = list(cos2 = 0.5), # Sélectionner les variables avec cos² > 50%
                repel = TRUE, # Éviter le chevauchement des étiquettes
                title = "Biplot des Individus et des Variables (cos² > 50%)",
                col.ind = "blue", # Couleur des individus
                col.var = "red", # Couleur des variables
                geom.ind = "point"  
)

5. Représentation des individus

Que révèle la position des individus sur le plan des deux premiers axes (proximité, similarité, groupes, outliers) ?

Nous analysons la position des individus (gènes) sur le plan des deux premières composantes principales de l’ACP (Dim1 et Dim2) afin de comprendre leur similarité, la formation de groupes et la présence d’outliers.

  • Deux gènes proches dans le plan ont des profils d’expression similaires sur les 12 conditions.

  • La distance euclidienne dans le plan factoriel reflète la similarité après réduction de dimension.

  • Gènes éloignés : expression spécifique ou extrême dans certaines conditions. Peuvent représenter des marqueurs spécifiques ou des variations expérimentales.

  • Le cos² mesure la qualité de représentation d’un gène sur le plan Dim1 × Dim2 :

    • cos² > 0.5 → bien représenté, interprétation fiable (on a uniquement représenté ces individus)

    • cos² faible → beaucoup de variance sur d’autres axes

En conclusion, la projection des gènes sur le plan factoriel permet de visualiser la structure globale des profils d’expression, d’identifier des groupes cohérents, et de mettre en évidence les gènes spécifiques ou outliers, tout en restant justifiée par la variance expliquée et le cos².

Ici beaucoup de points sont concentrés proche de l’origine, sachant que cos² > 0.5. La position est bien représentée sur ce plan. Autrement dit, la position à proximité de l’origine est fiable, pas un artefact dû au choix du plan. La plupart des individus (genes) ont donc une expression relativement constante à travers les conditions.

Références

Petropoulos, S., Edsgärd, D., Reinius, B., Deng, Q., Panula, S. P., Codeluppi, S., Reyes, A. P., Linnarsson, S., Sandberg, R., et Lanner, F. (2016). Single-cell RNA-seq reveals lineage and X chromosome dynamics in human preimplantation embryos. Cell 165: 1012‑1026.